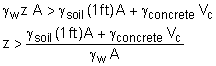| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Buoyancy | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Question 1 |
||
|
|
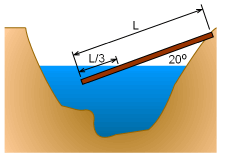
A wooden telephone pole paritally falls into a lake as shown. What is the density of the pole? Assume the density of the water is 1.94 slug/ft3. |
|
| Solution 1 |
||
The pole will come to a static position where the sum of the moments about the point O is equal to zero. ΣMo = 0 Therefore, the buoyancy force multiplied by its lever arm must be equal and opposite the gravitational force times its lever arm. ΣMo = 0 = (WpoleLpole - FBLB)cosθ where
WpoleLpole = FBLB where Wpole = ρpole V g = ρpole (π r2 L) g FB = ρwater V g = ρwater (π r2 L/3) g thus, ρpole (π r2 L) g (L/2) = ρwater (π r2 L/3) g (5L/6) Cancelling terms, ρpole (1/2) =(1.94 slug/ft3) (5/18) The density of the pole is ρpole = 1.078 slug/ft3 |
||
| Question 2 |
||
|
|
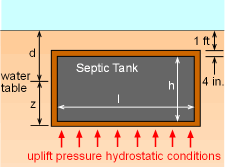
Septic tanks are used by homes in rural areas not serviced
by sanitary sewers. Assume the tank is 6 ft x 6 ft x 10 ft (long) with
4 in. concrete walls, and assume 1 ft of soil over the tank. At what
groundwater depth, d, if any, will the tank float? Any recommendations to
keep it from floating? Assume γconcrete = 150 pcf, γsoil = 120 pcf, and γwater = 62.4 pcf |
|
| Solution 2 |
||
Inside dimensions: h, w, l Vc = (h + 2t)(w + 2t)(l + 2t)
- hwl Since there is 1 ft of soil over the top of tank, z = (1 ft) + (h +2t) - d where d is the water table. To float, the buoyancy force acting on the bottom of the tank must be greater than the weight of the tank and the soil on top. septic tank: h = 6 ft, w = 6 ft, l = 10 ft, t = 4 in. Vc = 474.1 - 360 = 114.1 ft3 If the groundwater table depth is less than 1.89 ft, the septic tank will float. Recommendation to keep it from floating: use 6 in. walls instead of 4 in. |
||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.