| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Buoyancy | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
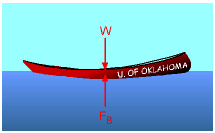
The total weight of the canoe and the paddlers is For equilibrium, the total weight must be balanced by the buoyant force. That is, W = FB The submerged waterline is denoted as h and the displaced volume for
each design will be expressed in terms of h as follows: |
|
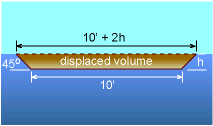
| For Design Layout A: |
||
|
|
The displaced volume of layout A is given by Applying force equilibrium yields 750 = (1.94) (32.2) (2) (10 + h)h Using the Quadratic Equation gives, h = 0.5678 ft The submerged height h (0.568 ft) is less than the height of the canoe (1 ft), hence this canoe will float. |
|
| For Design Layout B: |
||
|
|
The displaced volume of layout B is given by Applying force equilibrium yields 750 = (1.94) (32.2) (2) (11 + h)h The submerged height h (0.521 ft) is greater than the height of
the canoe (0.5 ft), hence this canoe will sink. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.