| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Hydrostatic Force -Curved Surface | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
Based on the methods developed for determining forces on a submerged plane surface in the previous section, forces exerted on a curved surface can be easily determined as given in this section. | |
|
||
| Hydrostatic Force on a Curved Surface |
||
|
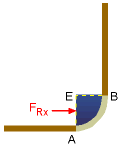
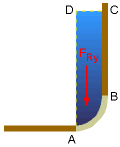
For a curved surface AB, as shown in the figure, the magnitude and the line of action of the resultant force FR exerted on the surface can be best derived by splitting the force into its horizontal and vertical components. The x-component of the resultant force FRx is the normal force acting on the vertical projection of the curved surface (i.e., surface AE). This force FRx passes through the center of pressure for the projected area AE. The y-component of the resultant force FRy is the weight of the liquid directly above the curved surface (i.e., volume ABCD). Note that this volume can be either real or imaginary. In this case, the volume is real since the liquid actually occupies this volume. Another example will be given later to illustrate an imaginary volume. This force, FRy ,passes through the center of gravity of volume ABCD. If the gravitational acceleration is assumed to be constant and the fluid is incompressible, then the center of gravity is the same as the centroid of the fluid volume. The magnitude of the resultant force is then determined by By inspection, it is noted that pressure forces are always perpendicular to the surface AB (i.e., the normal stresses). Since all points on a circle have a normal passing through the center of a circle, the resultant force FR has to pass through point E. The direction of the resultant force is given by θ = tan -1 (FRy / FRx) For non-circular shapes, the resultant angle is not used and the horizontal and vertical gravity center may not align with the actual surface. Again, it is easiest to keep the horizontal and vertical components separate in all calculations. |
||
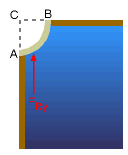 Concept of the Imaginary Volume |
Now consider another curved surface AB, as shown in the figure. The y-component of the resultant force is given by the weight of the liquid in a volume above surface AB (i.e., volume ABC); the volume in this case is an imaginary one since volume ABC is not occupied by an actual liquid. | |
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.