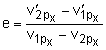| Ch 8. Rigid Body Momentum/Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse Momentum | Eccentric Impact | ||||||
| Eccentric Impact of Rigid Bodies | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
| Force of Impact |
||||||||
|
|
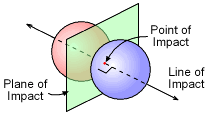
When two, free moving, rigid bodies collide, the force of the impact is directed perpendicular to the plane of impact when friction is neglected.The line of impact is perpendicular to the plane of impact as shown in the diagram. |
|||||||
| Coefficient of Restitution |
||||||||
 Coefficient of Restitution |
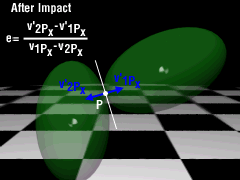
Like particle impact, the coefficient of restitution is defined by the relative velocities of the impact point for the two bodies,
It is important to note that these velocities are for point P in the line of impact, and not the center of gravity (cg) velocities. Also, this is a general simplification of real rigid body impact and does not include any frictional effects which can be considerable. The velocity of the impact point can be related to the cg velocity and its angular velocity through the relative velocity relationship |
|||||||
| Conservation of Linear Momentum |
||||||||
 Plane of Impact |
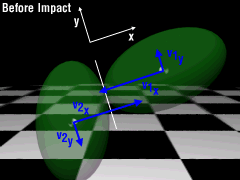
Similar to particle impacts, when two, free moving, rigid bodies collide, momentum is conserved. The velocity component parallel to the plane of impact (perpendicular to the line of impact) for each object remain unchanged since there is no collision in this direction. From the conservation of momentum, this gives,
However, the velocity component perpendicular to the plane (along the line of impact) will change. With no external forces, momentum in the x-direction must be also be conserved giving, Note, linear momentum is NOT conserved if one of the objects is pinned or constrained like a wall or floor. |
|||||||
| Conservation of Angular Momentum |
||||||||
 Angular Momentum During Impact for Object 1 |
For two, freely moving objects, angular momentum of each object is conserved about the impact point, P. This is not hard to realize since all forces due to impact act at P, and thus do not generate any angular impulse. In equation form, this relationship is
Since there are two objects, there will be two equations. Again, this only true if there are no applied moments about the point of impact, and there is no fixed point This can be expanded if rcg/p is the position vector of the center of mass relative to the impact point. Then the equation expands to Again, this scalar equation is valid for both objects since neither is pinned. This will give two equation, one for each object. In general, the above equations can be used to solve for the unknowns v'1x, v'1px, v'2x, v'2px, ω'1 and ω'2. |
|||||||
| Pinned Condition |
||||||||
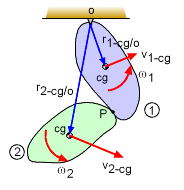 Impact with One Object Pinned |
A very common condition is when one of the objects is pinned, i.e. fixed point. In this case, the angular momentum of the complete system is conserved about that point (assuming there is no external forces or moments). However, the angular momentum of each object by itself is NOT conserved. And, the linear momentum is not conserved (very important). The total angular momentum about the pinned point, o, for all objects is, Σho-i = Σh'o-i This equation for the system can be expanded for two objects as But, angular momentum a single object is not conserved, only the total angular momentum of the system about the pinned point is conserved. Since the system has a pinned point (zero linear velocity), this equation can be further reduced to The derivation is not shown, but moment of inertia is moved to the pinned point and this will cancel out the linear velocity crossed with the position vector. |
|||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.