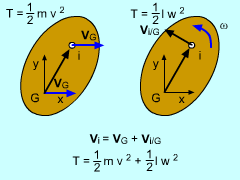| Ch 7. Rigid Body Energy Methods | Multimedia Engineering Dynamics | ||||||
| Rot. Work & Energy | Conservation of Energy | ||||||
| Rotational Kinetic Energy and Work | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||||||||||||
| General Work |
|||||||||||||||
|
|
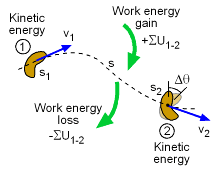
The Principle of Work and Energy equates the total work performed on a body to the change in kinetic energy, Σ Work = Δ Kinetic Energy Another way to express this concept is where Work on a rigid body is the same as work on a particle, with the addition of rotational energy. Recall from Particle Energy Methods section, there are various ways to model energy for a particle. These are listed in the table at the left. |
||||||||||||||
 Rotating Rigid Body |
Work of a Force Couple, or Moment |
||||||||||||||
|
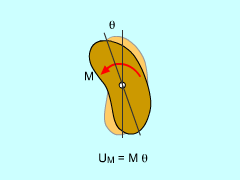
The work of two parallel, non-collinear forces in opposite directions with equal magnitudes forms a couple and moment. This moment generate energy similar to a linear force through a distance. However, the distance is now the angle of rotation.
|
|||||||||||||||
| Kinetic Energy for a Rotating Body |
|||||||||||||||
|
|
For a particle that has no rotation, the kinetic energy is simply, T = 1/2 m v2 This equation can be applied to every particle that makes up a rigid body, However, if the particle is a rigid body with dimensions, then the velocity needs to be written as where G is the center of gravity. The second terms models the rotation of the object. Substituting vi into the kinetic equation and noting that a magnitude of vi/G = ri/G ω gives If the rigid body has a fixed point, then the equation becomes T = 1/2 Io ω2 where Io is moment of inertia about the fixed point. |
||||||||||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.