| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotating Coordinates: Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
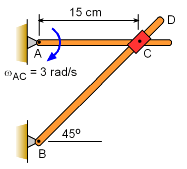 Two Connected Bars |
Example |
|
|
Two bars are pinned at one end, and connect with sliding collar at the other end. If the angular velocity of bar AC is clockwise at 3 rad/s, what is the angular velocity of bar BD? Point C slides smoothly along bar BD but is pinned to bar AC 15 cm from point A. .
|
||
| Solution |
||
|
|
Since the distance BC is not constant, this problem is well suited for using two frames of reference. Fix the local frame of reference, x-y, on bar BCD so that the motion of C can be easily modeled relative to B, (rC/B)rel. Then the velocity of C is, This equation includes the unknown angular velocity of bar BD, Ω = ΩBC = ΩBD, that is required, and can be determined. The global frame of reference is fixed to the background and is not moving. The velocity of B is zero (it is pinned). The velocity of C with respect to B, vC/B, is The velocity of point C, based on the motion of bar AC, in the global coordinate system is The relative position of C with respect to B is Putting all the terms together, gives -0.45J = -0.7071vC/BI - 0.7071vC/BJ + ΩBD = 1.50 rad/s |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.