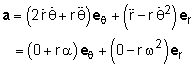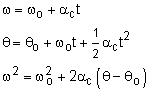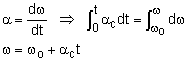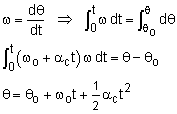| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotation about a Fixed Axis | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||
|
|
Unlike particle motion, rigid bodies can rotate and translate. This means both linear and angular velocities need to be analyzed. All general two-dimensional plane motion can be separated into rotating and translating motion. The rotating motion is commonly referred to as "rotation about a fixed axis". The two animations to the right show both rotational and translational motion. A good example of combined rotational and translational motion is the piston connecting rod. The arm moves back and forth but also rotates about the crank shaft, as illustrated in the animation below. |
|||||||||||||
|
|
Fixed Rotation of a Rigid Body |
|||||||||||||
|
|
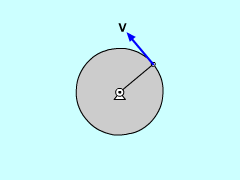
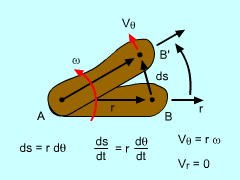
It is easier to solve problems when the translation and rotation components of motion are separated. By definition, a rotating body will have a point that has zero velocity which is its point of rotation (it can be on or off the object). If the body is pinned, this point is easy to identify. If not pinned, then this point can move as the object moves. For rotating bodies, there is no radial motion (the point is always rotating in a circle), and there is only motion in the tangent direction. Of course, the tangent direction can change for rotating objects that are not physically pinned. This type of motion is best described in polar coordinates. Recall from the Polar Coordinate section, velocity can be described as v = r ω eθ + dr/dt er The tangential velocity will be the angular velocity, ω (=dθ/dt), times the radial distance to the point and will only be in the tangent direction. The radial velocity will be zero since it is pinned. This simplifies the velocity to, |
|||||||||||||
|
Likewise, the acceleration for a point on a rotating object can be described using polar coordinate. The acceleration for a point on a rotating object will have two components, the θ and the radial direction. However, there will be no radial velocity or radial acceleration terms (i.e. dr/dt = d2r/dt2 = 0). The polar acceleration terms become, |
|||||||||||||
|
Constant Angular Acceleration |
|||||||||||||
|
Similar to constant linear acceleration, angular acceleration can be integrated over time to give angular velocity as a function time. If the acceleration is constant, then the equation becomes,
Integrating again gives angular rotation as a function of time, Both equations can be combined to eliminate time. All three equations are summarized at the left. |
|||||||||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.