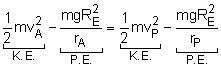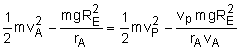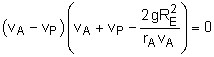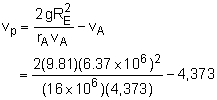| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Angular Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
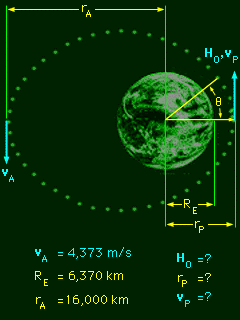 Re-entry of the Apollo Space Craft |
First, determine the angular momentum at apogee since the distance and space craft velocity is known at that point. (Ho)A = r × mv = m|r||v| sinθ ez = (16,000 x 103 m) (18,000 kg) = 1.26 x 1015 ez kg-m2/s Since the gravitational force acting on the Apollo is always directed towards the center of the earth, and the Apollo moves in a plane, it is in plane central-force motion. Thus, angular momentum about the center of the earth is conserved, and the angular momentum at all points in the orbit are the same, (Ho)P = (Ho)A = 1.26 x 1015 ez kg-m2/s |
|
| Distance and Speed at Perigee |
||
|
|
Because the Apollo space craft is in plane central-force motion, the product of its radial distance from the center of the earth and the transverse component of its velocity remains constant, giving rA vA = rP vP With two unknowns, a second equation is needed. Since gravity is the only force acting on the Apollo, the total energy must be conserved. Thus, the sum of the potential energy and kinetic energy is constant, Notice, the potential energy terms (P.E.) are negative. When working with potential energy in space, the datum line is assume to be at a large distance from the planet where there is no gravity and PE equals 0. Solve both equations simultaneously to determine the radius and speed at perigee. rP = rA vA /vP Substituting, This reduces to the quadratic equation which yields the trivial solution (circular orbit) vP = vA and the solution for the speed at perigee: vP = 7,000 m/s Substituting back into the original equation, gives the radius at perigee as rp = 10,000 km |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.