| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Relative Motion | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
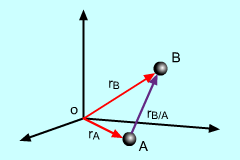 Adding Position Vectors |
In many situations, there is a need to examine the motion of two or more points relative to each other. Consider two points, A and B, both in motion relative to the origin O. This section will examine the motion of B relative to A. |
||||
| Position |
|||||
|
If rB/A is the position vector of B relative to A, then it can be stated that This is simply adding two position vectors to get a new total vector. This is illustrated in the diagram at the left. |
|||||
| Velocity |
|||||
|
To find the relative velocities of two points, take the time derivative of the position, giving d(rB)/dt = d(rA + rB/A)/dt |
|||||
| Acceleration |
|||||
|
Relative acceleration is found by taking the time derivative of the velocity, d(vB)/dt = d(vA + vB/A)/dt |
|||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.