| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Line Motion: Acceleration with time | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
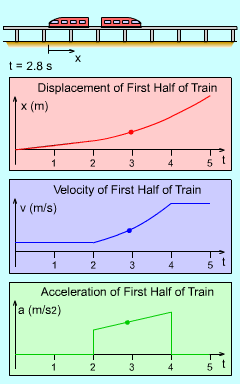 Train Motion |
When integrating the acceleration to determine the velocity and position, the initial conditions must be specified. The lower limits of integration will be vo = 50 m/s to = 2 s When the acceleration is integrated, the expression for the velocity, as a function of time, becomes v(t = 4) = 62 m/s The next step is to integrate the velocity. However, it is important that v(t) is integrated and not the velocity at 2 seconds, 62 m/s. This is a common mistake. Integrating the velocity function, v(t), gives an expression for the position as a function of time, x(t = 4) = 110.7 m Note that the initial position xo was set to zero when to = 2 so that the equation for x(t) gives the change in position starting at t = 2. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.