| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotating Coordinates: Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
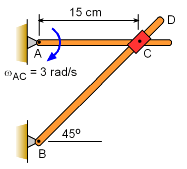 Two Connected Bars |
Example |
|
|
Two bars are pinned at one end, and connect with sliding collar at the other end. If the angular velocity of bar AC is clockwise at 3 rad/s, what is the angular velocity of bar BD? Point C slides smoothly along bar BD but is pinned to bar AC 15 cm from point A. .
|
||
| Solution |
||
|
|
Since the distance BC is not constant, this problem is well suited for using two frames of reference. Fix the local frame of reference, x-y, on bar BCD so that the motion of C can be easily modeled relative to B, (rC/B)rel. Then the velocity of C is, This equation includes the unknown angular velocity of bar BD, Ω = ΩBC = ΩBD, that is required, and can be determined. The global frame of reference is fixed to the background and is not moving. The velocity of B is zero (it is pinned). The velocity of C with respect to B, vC/B, is The velocity of point C, based on the motion of bar AC, in the global coordinate system is The relative position of C with respect to B is Putting all the terms together, gives -0.45J = -0.7071vC/BI - 0.7071vC/BJ + ΩBD = 1.50 rad/s |
|