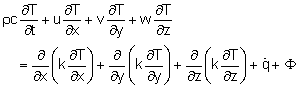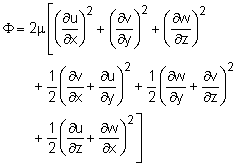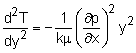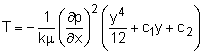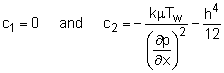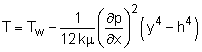| Ch 5. Fundamental Laws (Differential) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Navier-Stokes and Euler's |
Conservation Energy |
|||||
| Conservation of Energy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
The energy equation in differential form will be presented in this section. The details of the derivation are omitted, with attention focused on the use of the equation. |
|||||
| Energy Equation |
|||||
|
As discussed in the Conservation of Energy section, the energy equation is derived based on the first law of thermodynamics, which states that energy can neither be created nor destroyed; it can only change form. Similar to the derivations applied to derive the continuity and Navier-Stokes equations, the energy equation can be obtained by applying the first law of thermodynamics on a small differential fluid element. The derivation details are omitted for simplicity, and the energy equation for an incompressible fluid is given by where c is the specific heat, T is the temperature, k is the thermal conductivity, The energy equation expressed in terms of Cartesian coordinates is where the viscous dissipation function is given by As mentioned in the Moment of Momentum section section, there are three heat transfer modes: heat conduction, heat convection and radiation. The left hand side of the energy equation represents the local and convective terms, while the first three terms on the right represent the conductive terms. From the energy equation, it is noted that in order to solve for the temperature distribution, the velocity distribution is needed, which makes the analysis complex and tedious. Often, numerical methods such as finite difference and finite element methods are used to tackle these problems. However, analytical solutions do exist for some specific cases, and one such example is discussed next. |
|||||
| Flow between
Fixed Parallel Plates: Temperature Analysis |
|||||
|
|
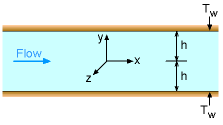
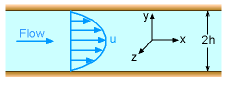
Consider steady, incompressible, laminar flow between two infinite parallel horizontal plates as shown in the figure. The velocity profile is found to be, where ∂p/∂x is treated as a constant and represents the pressure drop along the channel length. The velocity profile is parabolic, and it is a function of y only (as shown in the figure). Suppose that both plates are maintained at the wall temperature Tw, the temperature profile of the fluid can then be obtained from the energy equation. Assume that the plates are wide enough such that the temperature variation is only in the y-direction. The steady-state energy equation reduces to where the thermal conductivity is assumed constant. Substitute du/dy from the obtained velocity profile into the energy equation and rearrange terms to yield The above equation can then be integrated twice to obtain where the constants c1 and c2 can be determined from the temperature boundary conditions (i.e., T = Tw at y = h and -h) such that |
||||
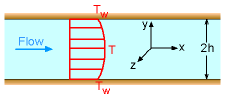 Temperature Profile |
The temperature profile is thus given by |
||||