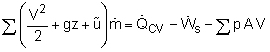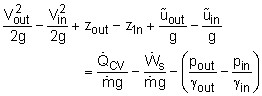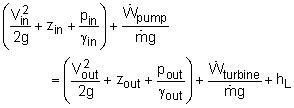| Ch 4. Fundamental Laws (Integral Anal.) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Linear Momentum |
Moment of Momentum |
Conservation Energy |
||||
| Conservation of Energy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
The first law of thermodynamics will be briefly introduced in this section. The energy equation for a control volume is given in integral form along with a discussion of the concept of total energy, heat and work. |
|||||
| Energy Equation (First Law of Thermodynamics) |
|||||
|
|
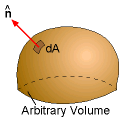
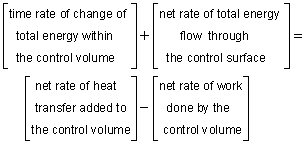
According to the first law of thermodynamics, energy can neither be created nor destroyed. It can only change forms. Similar to the conservation of mass, this concept can be modeled as a set of integral terms, one for the control volume, and one for the control surface. However, unlike the conservation of mass, new energy can be added or subtracted from the system through heat and work. The final integral form of the energy equation for a control volume is given by where e is the specific total energy (energy per unit mass), V is
the velocity of the fluid, Basically, the energy equation states that: which is equivalent to the first law of thermodynamics. For steady flow, the first term on the left hand side of the energy equation vanishes. The sign on the quantity V·n depends on the velocity as well as the orientation of the control surface. The unit normal vector is defined as positive when pointing out of the control surface. Hence, the term V·n will be positive when the flow is out of the control volume. This is similar to the momentum integral equation developed previously. For steady flow and constant area (assuming V and n are perpendicular, such as pipe inlet and outlet, the energy equation becomes |
||||
| Total Energy |
|||||
 Kinetic and Potential Energy |
The total energy term, e, needs special explanation. The total energy (E) stored in a system exists in three basic forms: kinetic energy (KE), potential energy (PE), and internal energy ( The above relation can also be expressed in terms of per unit mass simply by dividing by the mass, The specific kinetic energy is the energy associated with the motion of the system, and is similar to particle energy developed in dynamics. It is given by ke = V2/2 The specific potential energy is the energy associated with the elevation of the system with respect to an arbitrarily chosen reference plane: pe = gz The specific internal energy is the sum of all microscopic forms of energy (e.g., molecular or atomic energy) that a system possesses. Now, the energy equation becomes (recall, dm/dt = ρVA) |
||||
|
|
Heat |
||||
Heat transfer is energy transfer due to a temperature difference. Heat
is always transferred from the high temperature region to the low temperature
region. Heat transfer is considered positive when it is added to the
control volume, while it is negative when heat escapes from the control
volume. When
a control volume is said to undergo an adiabatic process, that means
heat transfer does not occur (i.e., There are three modes of heat transfer: conduction, convection and radiation. Heat transfer by conduction is mainly through the contact of two bodies, and it can occur in solids, liquids and gases. For example, heat is conducted from the heated stove to the pot, as shown in the figure. Heat transfer by a fluid in motion is referred to as convection. The motion of the fluid can be created artificially (forced convection) or naturally due to density differences (free convection). Heat transfer through electromagnetic waves is called radiation. The energy of the sun reaches the earth by radiation. Generally, heat is not involved for basic fluid mechanic problems and is generally 0. However, it should be noted viscous effects will generate heat, and they must be included. |
|||||
|
|
Work |
||||
Work is the energy transfer associated with a force acting through a distance. Work done by the control volume is considered positive. Examples of work include flow work and shaft work. When a fluid flows through a control volume, flow work arises due to the pressure forces exerted on the inlets and outlets. The flow work is given by where p is the pressure, A is the cross-sectional area, and V is the velocity of the fluid. If the velocity is perpendicular to the surface, dA, and A is constant, then this simplifies to The work due to pressure can be both positive or negative depending if the pressure is acting with the flow (negative, n·V = -V) or against the flow (positive). Shaft work is encountered frequently in engineering applications (e.g., turbines or the power transmission of a car), and it is given by where T is the torque of the shaft , and ω is the angular velocity of the shaft. For example, shaft work produced from turbines is converted to electricity through generators in hydroelectric power plants. Power out would be positive, like a turbine. Combining heat and work terms, the steady state energy equation becomes |
|||||
| Steady Energy Equation with Inlet and Outlet |
|||||
 Steady Energy Equation with Inlet and Outlet |
A common application of the steady state energy equation is for a control volume with inlets and outlets. Using the subscripts 'in' and 'out' to describe flow into the system, respectively, and dividing by g(dm/dt) gives The u and Q terms are usually grouped together, and simply labeled as 'head loss', hL, This includes all viscous effects such as flow through pipes. Also accounts for piping and inlet/outlet edge energy loss mainly due to viscous flow. It is also useful to split the work as a pump (energy in) and a turbine (energy out). The final form is
where the subscript 'pump' represents energy being supplied into the system and 'turbine' represents energy being removed (to do useful work). Both terms is absolute energy in or out and does not consider the efficiency of the pump or turbine. In a practical application, the internal energy loss of the pump or turbine needs to be taken into account. This equation assumes just one inlet and one outlet for a control volume, and steady state. This equation is similar to the famous Bernoulli's Equation but includes work and viscous effects. |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.