Ch 5. Beam Deflections     Multimedia Engineering Mechanics
Integration
of Moment		 Integration
of Load		 Method of
Superposition		 Indeterminate
Beams		    
Mechanics
 Integration of Moment Equation Case Intro Theory Case Solution Example
 Chapter
 1. Stress/Strain
 2. Torsion
 3. Beam Shr/Moment
 4. Beam Stresses
 5. Beam Deflections
 6. Beam-Advanced
 7. Stress Analysis
 8. Strain Analysis
 9. Columns
 
 Appendix
 Basic Math
 Units
 Basic Mechanics Eqs
 Sections
 Material Properties
 Structural Shapes
 Beam Equations
 
 eBooks
 Dynamics
 Fluids
 Math
 Mechanics
 Statics
 Thermodynamics
 
©Kurt Gramoll
MECHANICS - EXAMPLE
    Example

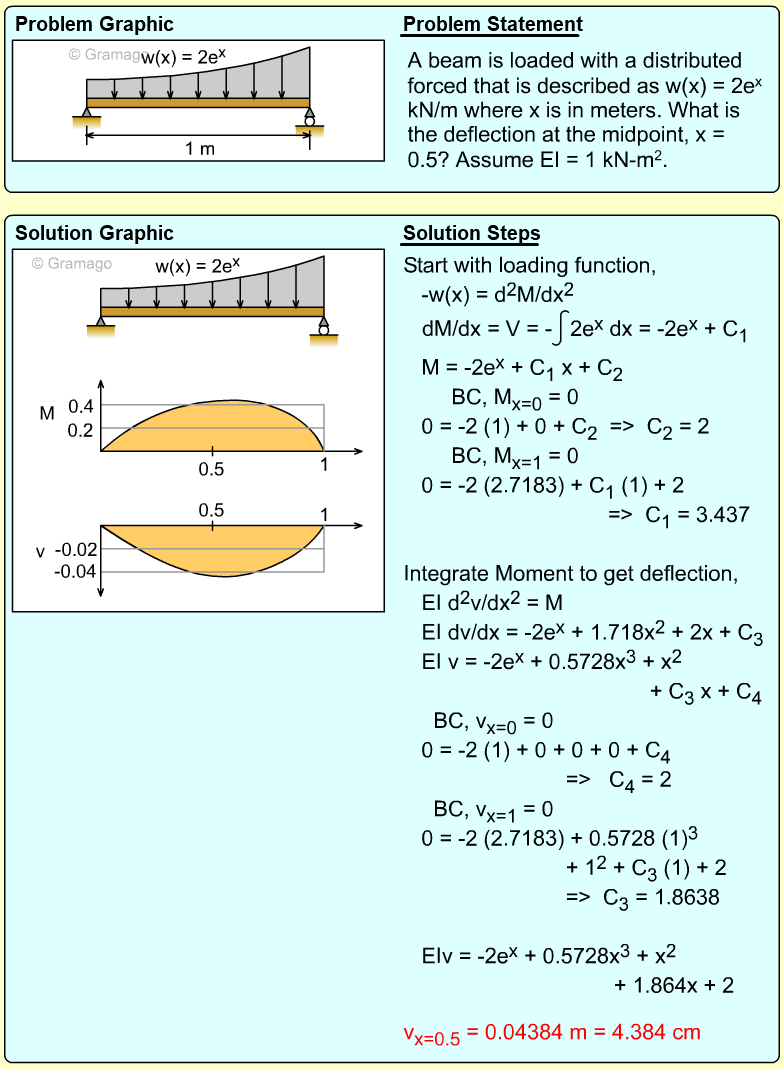
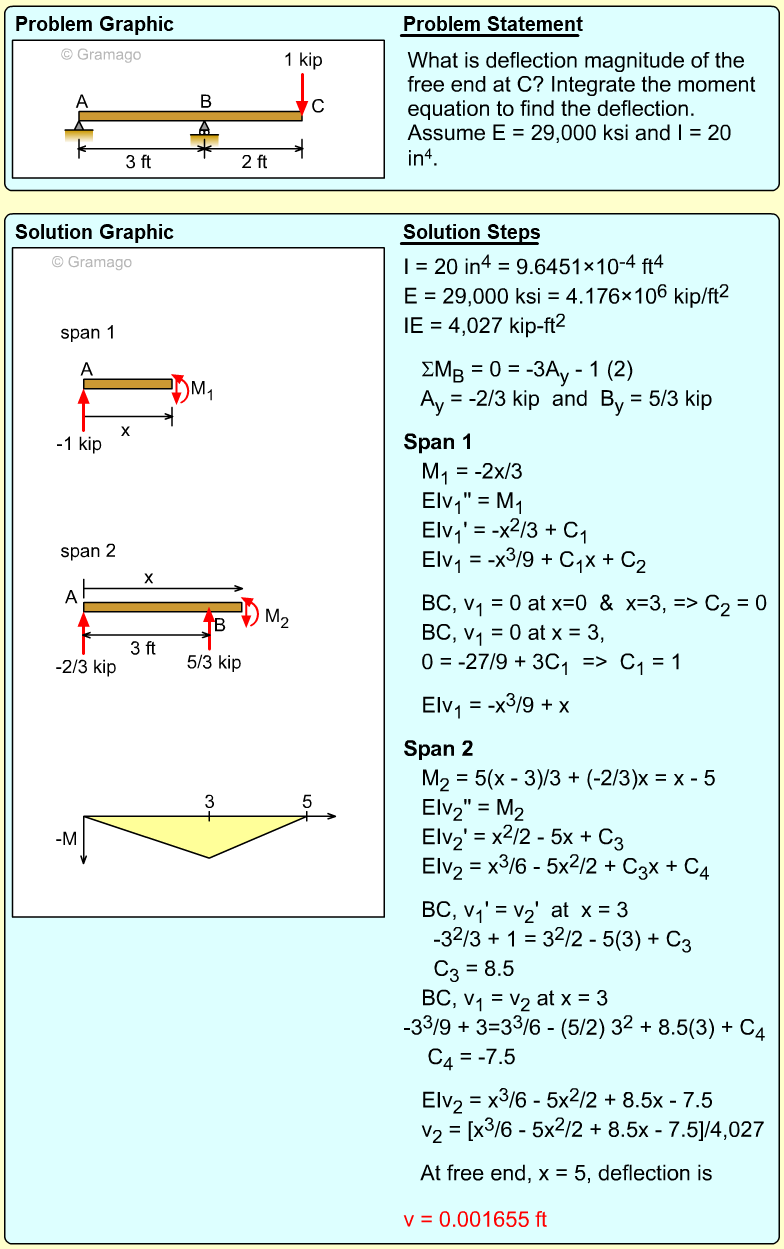
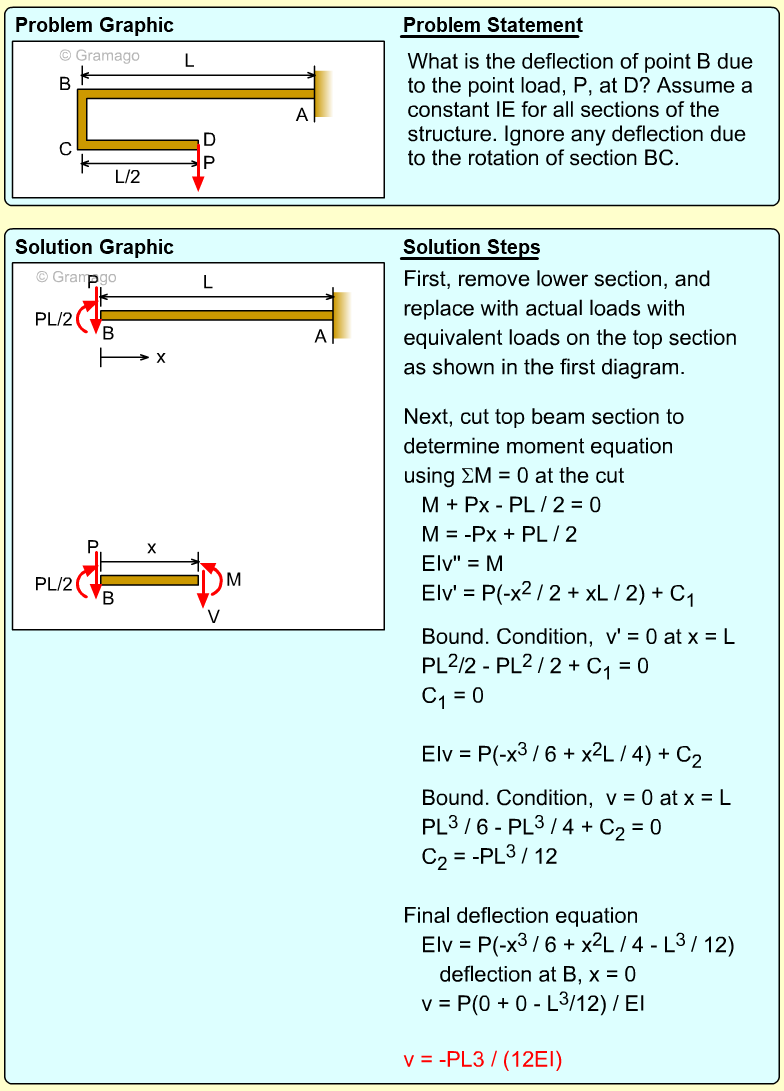
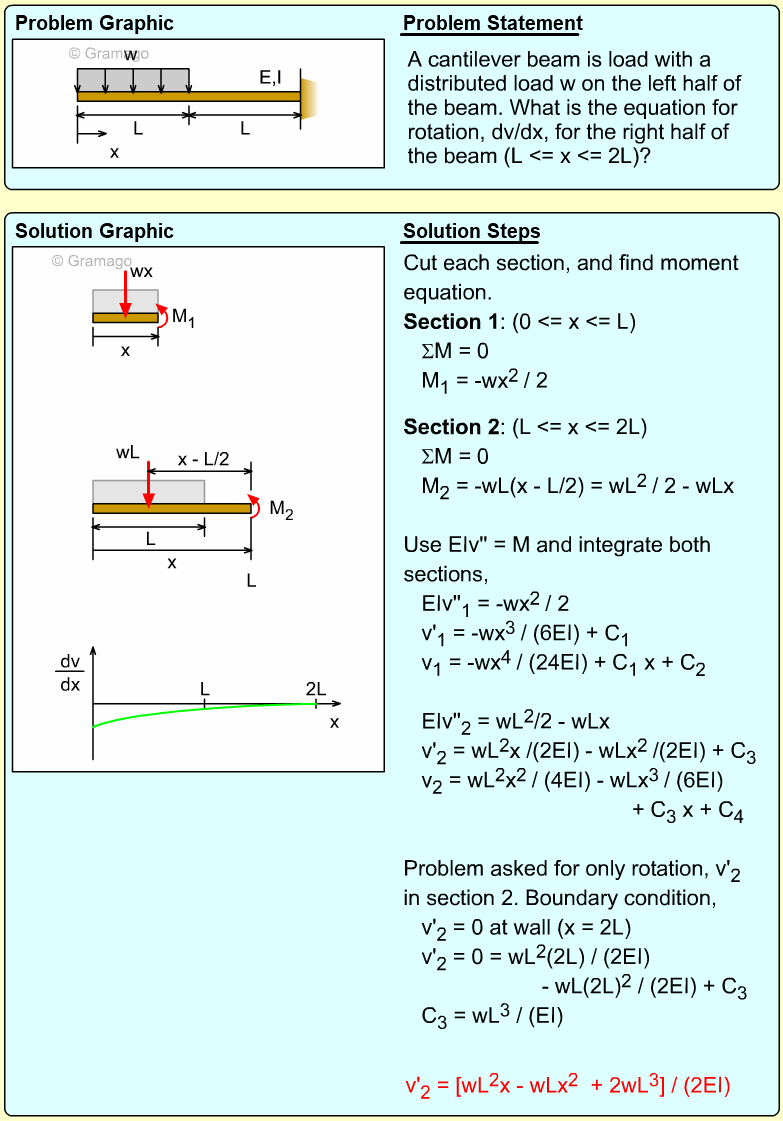
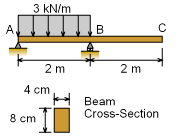Partially Loaded Beam 		 

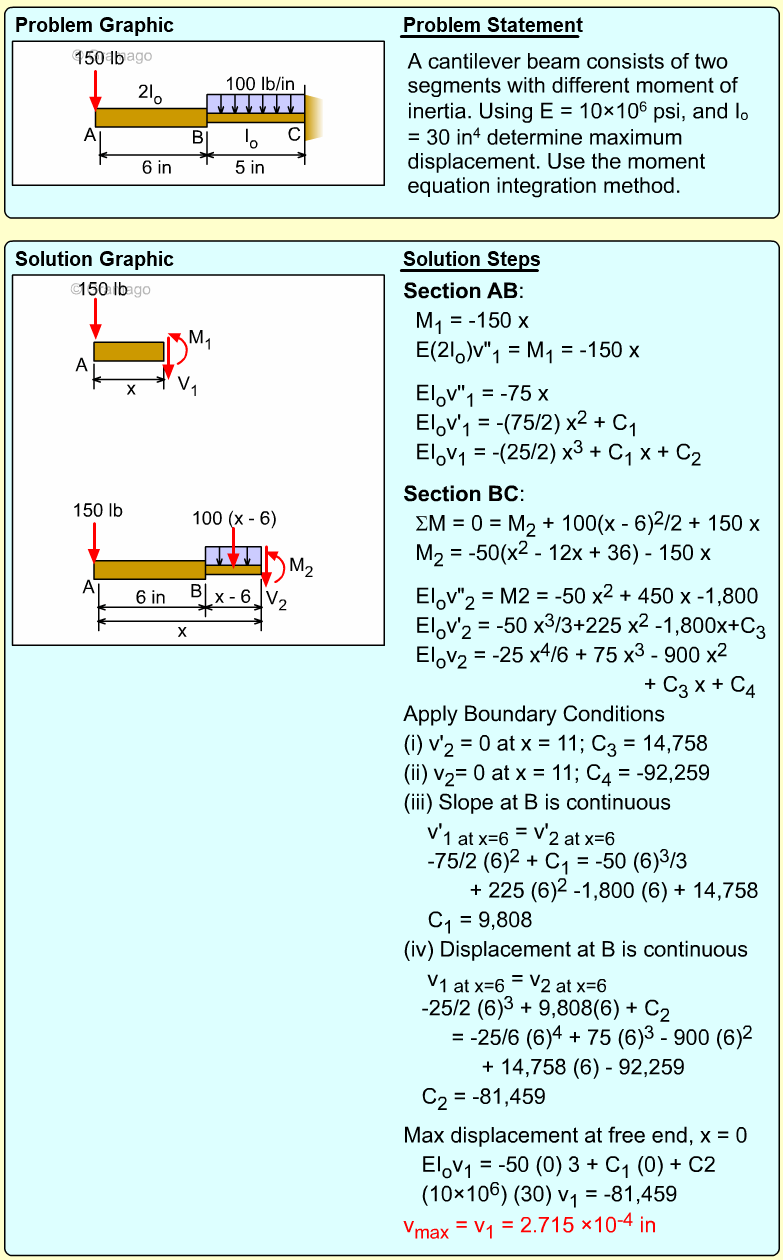
Beams commonly have distributed loads over only sections of the total beam, similar to the beam shown in the diagram. In this case, what is the deflection of the far right end (point C)? Assume the modulus of elasticity, E, is equal to 10 GPa.

   
  Solution

 

  

There are two basic ways to solve this problem using integration. First, the moment in both beam sections, AB and BC, can be determined, and then integrated using two boundary conditions for each span.

A second, and easier method, would be to find the rotation angle at B, and then just extrapolate the deflection from B to C. This is possible since there are no loads on the beam section BC and thus there will be no bending. The section BC will rotate, but it remain a straight line. Of course, the rotation at B still needs to be determined by integrating the moment equation, but it is only one equation instead of two equations needed in method 1.

     

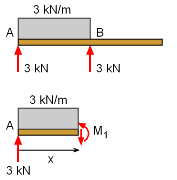Beam Support Reactions 		 

Due to symmetry, each of the two supports will carry half the load, giving,

     Ay = By = 3(2)/2 = 3 kN

The moment equation for the first span, AB, is found by cutting the span at distance x from the left, and summing moments. This gives,

     M1 + 3x(x/2) - 3x = 0
     M1 = 3x - 1.5x2 kN-m

Now that the moment equation is known for the span, it can be integrated once to find the beam rotation, and a second time for beam deflection,

     

The deflection, v1, for the span AB is know at x = 0 and x = 2 m. Using these two boundary conditions, gives

     v1(x=0) = 0.5 (0)3 - 0.125 (0)4 + C1 (0) + C2
          ==> C2 = 0

     v1(x=2) = 0.5 (2)3 - 0.125 (2)4 + C1 (2) + 0
          ==> C1 = -1

This give the beam rotation as

     EIv' = (1.5x2 - 0.5x3 -1) kN-m2
     

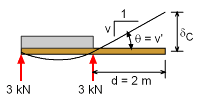Beam Deflection at Point C 		 

The beam moment of inertia, I, is

     I = 83(4)/12 = 170.7 cm4 = 170.7e-8 m4
and
     EI = (10e9 N/m2)(170.7e-8 m4 ) = 17.07 kN/m2

The beam rotation at B is

     v'(x=2) = (6 - 4 -1)/EI
               = (1 kN-m2)/(17.07 kn-m2)
               = 0.05858 radians

The final deflection at C can be determined by noting that that beam rotation at B is also the slope at B. The final deflection is just the angle (or slope) times the distance,

      δC = θ d =0.05858 (2 m)

         = 0.1172 m