Force Equilibrium

Submerged Water Line

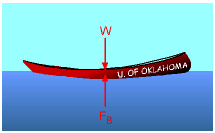
The total weight of the canoe and the paddlers is
     W = 120 lb + 630 lb = 750 lb

For equilibrium, the total weight must be balanced by the buoyant force. That is,

     W = F_B

where the buoyant force is the weight of the liquid displaced by the volume and is given by

     F_B = ρgV_displaced

The submerged waterline is denoted as h and the displaced volume for each design will be expressed in terms of h as follows:

Displaced Volume of Design Layout A

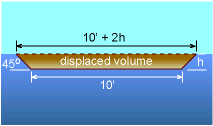
The displaced volume of layout A is given by

     V_displaced = 2 (10 + h) h

Applying force equilibrium yields

     750 = (1.94) (32.2) (2) (10 + h)h
     h² + 10h - 6 = 0

Using the Quadratic Equation gives,

     h = 0.5678 ft

The submerged height h (0.568 ft) is less than the height of the canoe (1 ft), hence this canoe will float.

Displaced Volume of Design Layout B

The displaced volume of layout B is given by

     V_displaced = 2 (11 + h) h

Applying force equilibrium yields

     750 = (1.94) (32.2) (2) (11 + h)h
     h² + 11h - 6 = 0
     h = 0.5208 ft

The submerged height h (0.521 ft) is greater than the height of the canoe (0.5 ft), hence this canoe will sink.