| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Normal/Tangential Coordinates | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
|
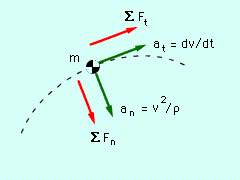
Previously, in the Curvilinear Motion: Normal/Tangential Coordinates section in chapter 1, equations for the normal and tangential components of acceleration were derived for a particle moving in a plane curved path. These were, at = dv/dt an = v2/ρ Newton's Second Law can also be expressed in terms of normal and tangential coordinates, ΣFtet + ΣFnen = m (atet + anen ) Substituting gives, ΣFtet + ΣFnen = m (dv/dtet + v2/ρen ) Or for just the tangent direction, ΣFt = m dv/dt In the normal direction, ΣFn = m v2/ρ |
||||