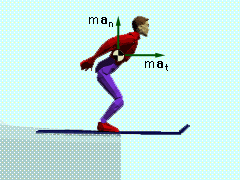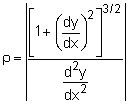| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Normal/Tangential Coordinates | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
|
|
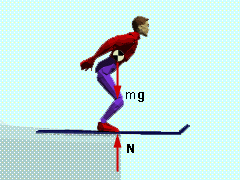
Using the principle of conservation of energy, the velocity of the skier at the end of the jump can be found. Energy is a simple way to find the velocity of any object if you know how far it falls. Of course, this method neglects air and surface friction which is lost energy. The principle of conservation was introduced in your basic physics course, and will studied in detail in the section on conservative forces and potential energy. Equating the potential of the skier at the top of the jump with the kinetic energy at the bottom of the jump gives Upotential = Ukinetic If the velocity at the bottom of the jump is noted as v2, then The free-body and mass-acceleration diagrams are shown at the left. Summing the forces in the normal direction gives ΣFn = man N - mg = m v2/ρ To solve for the normal force, N, the radius of curvature, ρ, must be determined at the
end of the jump. From calculus, the radius of curvature for any continuous line
function, y = f(x), is For this problem, |
|
 Velocity of Skier |
Thus, at x = 0,
Using the radius of curvature, the normal force exerted on the skier at the end of the jump is N = m v2/ρ + mg |
|
| Solution of b) |
||
 Acceleration of Skier |
To find the total acceleration of the skier, sum the forces in the tangential direction, ΣFt = mat 0 = mat Thus, the acceleration at the end of the jump in the tangential direction is zero. The total acceleration is a = an en + at et |
|