| Ch 1. Basics | Multimedia Engineering Fluids | ||||||
|
Mass Density |
Ideal Gas Law |
Viscosity |
Surface Tension |
Vapor Pressure |
|||
| Viscosity | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||
|
Another important fluid property will be introduced in
this section. Viscosity is a fluid property that measures the resistance
of
the fluid
due to
an applied force. |
||||||||||||||||||||||||||
|
|
Viscosity |
|||||||||||||||||||||||||
|
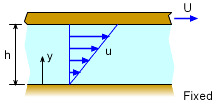
To illustrate the concept of viscosity, consider a fluid between two parallel plates, as shown in the figure. If the top plate is moved at a velocity U while the bottom plate is fixed, the fluid is subjected to deformation. The fluid in contact with the top plate moves with the plate velocity U and no-slip condition is applied at the bottom plate (i.e., the fluid is stuck to the bottom plate, u = 0). The velocity profile of the fluid motion between the plates is assumed to be linear and is given by u = U y/h Note that the velocity gradient (also known as the rate of shear strain) in this case is a constant (du/dy = U/h). Experiments have shown that shear stress (τ) is directly proportional to the rate of shear strain: |
||||||||||||||||||||||||||
|
Most common fluids, such as water, air and oil, are called Newtonian fluids in which the shear stress is related to the rate of shear strain in a linear fashion. That is, The above equation is referred to as Newton's law of viscosity. The proportionality constant (μ) is called the absolute viscosity, dynamic viscosity or simply the viscosity. It has units of N-s/m2 in SI units (lb-s/ft2 in US units). Sometimes it is also expressed in the CGS system as dyne-s/cm2 and this unit is called a poise (P). Note that the shear stress can also be determined by dividing the shear force with the surface area. |
|||||||||||||||||||||||||
 Shear Thinning Fluid: Latex Paint |
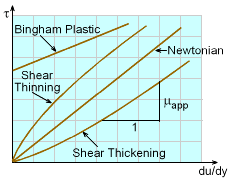
For non-Newtonian fluids, the shear stress is not a linear function of the rate of shear strain. Some common types of non-Newtonian fluids are shear thinning fluids, shear thickening fluids and Bingham plastic. To describe these non-Newtonian fluids, an apparent viscosity is introduced and it represents the slope (not constant) of the shear stress versus the rate of shear strain. It is obvious that for Newtonian fluids, the apparent viscosity is the same as the viscosity and is not a function of the shear rate. |
|||||||||||||||||||||||||
 Shear Thickening Fluid: Quicksand |
For shear thinning fluids, the apparent viscosity decreases with shear rate, whereas for shear thickening fluids, the apparent viscosity increases with shear rate. An example of a shear thinning fluid is latex paint. When brushing paint on a wall, note that the larger the applied shear rate, the less resistance that (viscosity) is encountered. Examples for shear thickening fluids are quicksand and a water-corn starch mixture. The larger the applied shear rate trying to mix water with corn starch, more resistance will be encountered. |
|||||||||||||||||||||||||
 Bingham Plastic: Toothpaste |
Another non-Newtonian fluid is Bingham plastic,
which is neither a fluid nor a solid. Bingham plastic, such as toothpaste, can
withstand a finite shear stress without any motion, however it moves
like a fluid once this yield stress is exceeded. Note that only Newtonian
fluids will be considered in the future discussion; non-Newtonian
effects are beyond the scope of this eBook. Viscosity is not a strong function of pressure, hence the effects of pressure on viscosity can be neglected. However, viscosity depends greatly on temperature. For liquids, the viscosity decreases with temperature, whereas for gases, the viscosity increases with temperature. For example, crude oil is often heated to a higher temperature to reduce the viscosity for transport. |
|||||||||||||||||||||||||
| Kinematic Viscosity |
||||||||||||||||||||||||||
|
The kinematic viscosity is the ratio of absolute viscosity and density. That is, ν = μ / ρ |
||||||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
 Shearing Stress
versus Rate of
Shearing Stress
versus Rate of