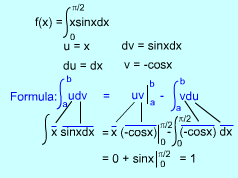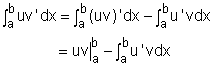| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Integration by Parts | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
This section introduces one of the general techniques
of integration, integration by parts. |
||
| Indefinite Integration by Parts |
||
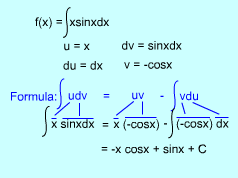 Integration xsinx using Integration by Parts (Indefinite Integration) |
If function u = u(x) and v = v(x) are differentiable functions, according to the Produce Rule, the differentiation of the product of functions u and v is (uv) ' = u 'v + uv ' Rearrange the above equation gives uv ' = (uv) ' - u 'v Integrating both sides (indefinite integrals), Since v' dx = dv, and u' dx = du, for simple, the formula for integration by parts becomes |
|
| Definite Integration by Parts |
||
|
Evaluating both sides of the previous equation between a and b, assuming u ' and v ' are continuous, becomes, The key in using integration by parts is how to choose u and dv. Two things should be considered,
|
|