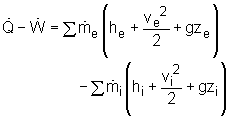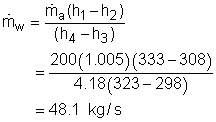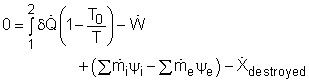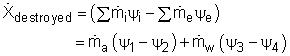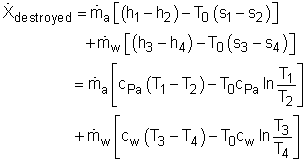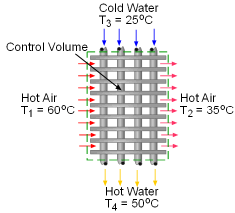
A heat recovery system is designed to heat cold water using the exhausted hot air from a subway station. Mass flow rate of the cold water, exergy destruction, and the second-law efficiency of the heat recovery system needs to be determined.

Assumptions:

• Model the water as incompressible substance with a density ρ = 1,000 kg/m³ and a specific heat c_w= 4.18 kJ/kg-K.
• The exhausted air is modeled as an ideal gas with a density ρ = 1.8 kg/m³ and a specific heat c_Pa = 1.005 kJ/kg-K.
• The heat recovery system is well insulated that the heat exchange process is adiabatic.
• No work interaction is involved.
• Neglect the kinetic and potential energy changes.
• The heat exchange process is an isobaric steady process.

Take the Heat Recover System
as a Control Volume

Consider the heat recovery system as a control volume and denote the hot air inlet as 1, hot air exit as 2, cold water inlet as 3, and hot water exit as 4, shown on the left.

(1) Determine the mass flow rate of the cold water

The energy balance for a control volume is:

According to the assumptions, the energy balance can be simplified to

Water is modeled as an incompressible substance. Thus, its enthalpy equals

      h₄ = c_wT₄ and h₃ = c_wT₃

Exhausted air is modeled as an ideal gas, its enthalpy equals

      h₂ = c_PaT₂ and h₁ = c_PaT₁

where T₁,T₂, T₃ , T₄ and are given as

      T₁ = 60^oC = 333 K
      T₂ = 35^oC = 308 K
      T₃ = 25^oC = 298 K
      T₄ = 50^oC = 323 K
      = 200 kg/s

Substituting all the data to the energy balance gives the mass flow rate of cold water.

(2) Determine the exergy destruction of the heat recovery system

The exergy balance of control volume undergoing a steady-flow process is

Since the heat recovery system is an adiabatic heat exchanger, it becomes

where ψ is the flow exergy. it is expressed as

      ψ = h - T₀s

Therefore, the exergy destruction can be rewritten as

Substitute all the data given to the above equation gives

(3) Determine the second-law efficiency of the heat recovery system

The definition of the second-law efficiency of a heat exchanger is