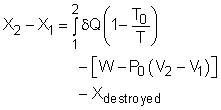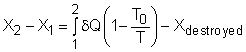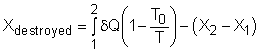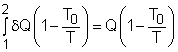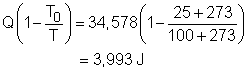Exergy destroyed by boiling an egg from 10^oC to 100^oC in 100^oC water needs to be determined.

Assumptions:

• Model both the egg and the water as incompressible substance.
• Constant-specific-heat assumption is valid for both the water and the egg.
• Kinetic and potential energy changes of the egg are negligible.
• No work interaction is involved.
• Water remains 100^oC during the cooking process.

Consider the Egg as a Closed System

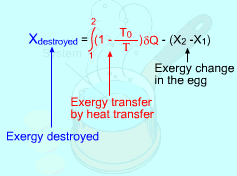
Take the egg as a system. It is a closed system since no mass flows in or out of the egg. The exergy balance for a closed system is:

where 1 denotes the initial state and 2 denotes the final state. The assumption states that no work interaction is involved, and the volume of the egg does not change during the cooking process since eggs are incompressible. Thus, the exergy balance can be simplified as

Rearranging the above equation gives the expression of the exergy destruction. That is,

The first term on the right hand in the above equation represents the exergy transfer by heat transfer. The egg is cooked from 10^oC to 100^oC in 100^oC water. Assuming the boundary of the egg remains at 100^oC during the whole process then this term can be simplified to

where T₀ is the ambient temperature and is given as 25^oC. T is the temperature at the boundary of the egg where heat transfer occurs. Hence,T is equal to 100^oC.

Q is the heat transferred to the egg from the water. Q can be determined by the energy balance of the egg. The egg is approximated as an incompressible substance and no work interaction is involved. With constant-specific-heat assumption, the energy balance is

      Q =  mc_ave (T₂ - T₁)

The mass of the egg is

      m = Vρ = 4/3(3.14)(0.03)³(1,000) = 0.113 kg

The average specific heat is given as 3.4 kJ/(kg-K).

Substituting all the data into the expression of energy balance yields

       Q = 0.113(3,400)(100 - 10) = 34,578 J

Substituting Q, T₀ and T to the expression of exergy transfer by heat transfer gives,

The second term on the right hand side of the exergy destruction is the exergy change in the egg during the cooking process. The exergy change of a closed system without kinetic and potential energy changes is:

      X₂ - X₁ = (U₂ - U₁) + P₀(V₂ - V₁) - T₀(S₂ - S₁)

Since the egg is incompressible, the second term in the right hand of the above equation equals 0. Also, the constant-specific-heat assumption is valid. The exergy change in the egg can be determined from

      X₂ - X₁ = mC_ave(T₂ - T₁) - T₀mC_aveln(T₂/T₁)

T₁ is the initial temperature and T₂ is the final temperature of the egg. They are given as

      T₁ = 10^oC = 283 K
      T₂ = 100^oC = 373 K

Substituting all the data into the expression of exergy change in the egg yields

      X₂ - X₁ = 0.113(3,400)(373 - 283) -
                  (25 + 273)(0.113)(3,400) ln(373/283)
                = 2,960.2 J

After calculating the exergy transfer by heat and the exergy change in the egg, the exergy destruction can be determined.

      X_destroyed = 6,953.0 - 2,960.2 = 3,992.8 J

Note: Another method to determine the exergy destruction is from its definition.

      X_destroyed = T₀S_gen

The entropy generation is 13.4 J/K. (See previous section to view how to determine the entropy generation). Thus, the exergy destruction is

      X_destroyed = T₀S_gen = (25 + 273)(13.4) = 3,993.2 J

which is almost the same as the one determined from the exergy balance.