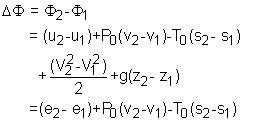| Ch 7. Exergy Analysis | Multimedia Engineering Thermodynamics | ||||||
| Exergy |
Exergy Change |
Exergy Balance(1) |
Exergy Balance(2) |
||||
| Exergy Transfer, Exergy Change | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Exergy Change of a System
|
||
| Exergy is a property, which depends on the state of the environment as well as the state of the system. Only thermo-mechanical exergy, which disregards any mixing and chemical reaction, will be discussed in this section. | ||
|
|
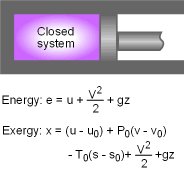
Exergy of a Closed System A closed system has a fixed mass. The total energy of a simple, compressible closed system is the sum of its internal, kinetic, and potential energies. Therefore, the exergy of such a system is the sum of the exergies of its internal, kinetic, and potential energies. The unit-mass form is, Φ = (u - u0) + P(v - v0)
- T0(s - s0)
+ V2/2 + gz The exergy change of a closed system during a process from state 1 to state 2 is |
|
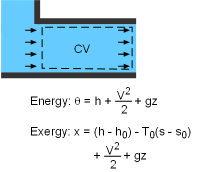 Exergy of an Open System |
Exergy of an Open System The total energy of a flowing fluid in a control volume is the sum of the enthalpy, kinetic energy, and potential energy. Therefore, the exergy of such a system is the sum of the exergies of its enthalpy, kinetic energy, and potential energy. The unit-mass form is, Ψ = (h - h0) - T0(s - s0) + V2/2 + gz The exergy change of a control volume during a process from state 1 to state 2 is |
|
| Exergy Transfer
|
||
|
|
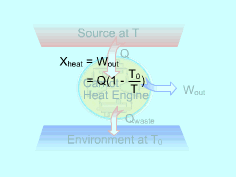
Exergy can be transferred to or from a system by heat, work, and mass. Exergy Transferred by Heat (Q) Work can be obtained from a heat source at temperature (T), which is above the environment temperature (T0), by transferring heat (Q) to a heat engine and rejecting the waste heat to the environment. Hence, heat transfer is always accompanied by exergy transfer. The maximum work that can be obtained from a heat source at temperature T is the work output from a Carnot heat engine which works between this heat source and the environment. The Carnot efficiency of Carnot heat engine is, ηth = 1-T0/T Therefore, the exergy of heat Q is, Xheat = Wnet,out = (1-T0/T)Q When the temperature at the location where heat transfer occurs is not a constant, the exergy transfer accompanying heat transfer is determined by integration. |
|
|
Exergy Transferred by Work |
Exergy Transferred by work (W) Exergy is the useful work potential. For boundary work, such as the expansion work of a piston-cylinder device, a portion of work is used to push the atmosphere air away and it cannot be utilized. Thus, the exergy transfer by the expansion work equals the difference between the expansion work and the surroundings work, that is, Xb = W - Wsurr where Other type of work, such as shaft work and electric work, can be completely utilized. Therefore, the exergy transfer by shaft work or electric work is equal to the work itself. XW = W |
|
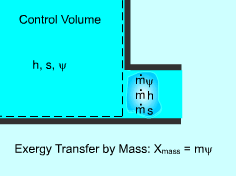 Exergy Transferred by Mass |
Exergy Transferred by Mass (m) Mass contains exergy as well as energy and entropy. The rate of exergy transfers to or from a system is proportional to the flow rate. When a mass (m) enters or leaves a system, exergy(mΨ) enters or leaves a system as well, where Ψ is the flow exergy. Xmass = mψ = m[(h - h0) -T0(s - s0) + v2/2 + gz] |
|
| The Decrease of Exergy Principle
|
||
|
|
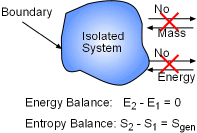
Consider an isolated system shown on the left. No energy or entropy transfer occurs at the boundary since no heat, work and mass transfer between the isolated system and its surroundings. The energy balance and entropy balance for the isolated system is: Energy
balance: E2 - E1 = 0 (1) Multiplying (2) by T0 and subtracting it from (1) yields, (E2 - E1) -T0(S2 - S1) = -T0Sgen (3) An Isolated system is also a closed system. Exergy change of a closed system is ΔX = X2 -
X1 Since no volume changes of the isolated system, the above equation becomes, ΔX = (E2 - E1) - T0(S2 - S1) (4) Compare (3) and (4) gives, -T0Sgen = X2 - X1 or Xisolated = -T0Sgen =
X2 -
X1 This equation shows that the exergy change of an isolated system during
a process is always smaller than zero or equal to zero while
the process is reversible. This is known as the decrease of exergy principle. |
|
| Exergy Destruction
|
||
Exergy Destruction |
When a system undergoes an irreversible process, the entropy always increases and anything that generates entropy always destroys exergy. X2 - X1 = -T0Sgen or Xdestroyed = T0Sgen |
|