| Ch 7. Exergy Analysis | Multimedia Engineering Thermodynamics | ||||||
| Exergy |
Exergy Change |
Exergy Balance(1) |
Exergy Balance(2) |
||||
| Exergy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||||||||
| Exergy
|
||||||||||||||||||||
|
|
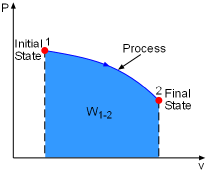
Work done during a process depends on its initial state, final state, and the process itself. That is, work = f(initial state, process, final state) If the initial state has been specified, then work is only a function of process and the final state. Previously, it was shown that reversible process between two selected states gives the maximum work output. What kind of final state can help the process reach its maximum work output? System exchanges work, heat, and mass with its surroundings during a process. If the system reaches a state which is in equilibrium with its surroundings, then the system can not exchanges work, heat, and mass with its surroundings. This state is called a dead state and its properties are denoted by subscript 0, such as pressure P0 and temperature T0. At the dead state:
|
|||||||||||||||||||
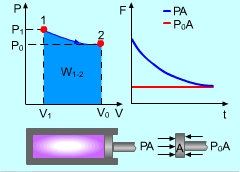 Gas Expanding in a Cylinder |
For example, gas expands in a cylinder to do work on its surroundings. If the pressure in the cylinder reaches the pressure in its surroundings, no more work can be done by the cylinder. That means the cylinder reaches its dead state, and the work done by this cylinder reaches its maximum value. Therefore, a system will deliver the maximum possible work if it undergoes
a reversible process from the specified initial state to its dead state.
This work represents the useful work potential of the system at the specified
initial state and is called exergy of the specified initial state. |
|||||||||||||||||||
| Irreversibility
|
||||||||||||||||||||
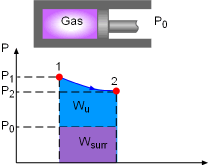 Useful Work, and Surrounding Work for Gas expanding |
Irreversibility is defined as the difference between the reversible work and the useful work. It is expressed as I = Wrev,out - Wu, out or I = Wu, in - Wrev,in where Wrev is the reversible work and Wu is the useful work. The definitions of reversible work and the usefully work are given below. When gas expands in a cylinder to do work, it needs to expend some work on pushing the atmospheric air out of the way. This part of work can not be recovered and utilized, and is called surrounding work, which is the work done by or against the surroundings during a process. For the gas expansion process, the surrounding work equals, Wsurr = P0(V2 - V1) where The difference between the actual work and the surrounding work is called useful work. It is expressed as Wu= W - Wsurr Reversible work is defined as the maximum amount of useful work that can be produced (or the minimum work consumed) as
a system undergoes a process between the specified initial and final states. |
|||||||||||||||||||
| Exergy
Associated with ke, pe, u, Pv, and h |
||||||||||||||||||||
A system can contain energy in numerous forms such as kinetic energy, potential energy, internal energy, flow work and enthalpy.
Exergy is the useful work potential of energy, and the exergy of a system is the sum of the
exergies of different forms of energy it contains. The relations between
the Exergy associated with different energy forms are developed below. |
||||||||||||||||||||
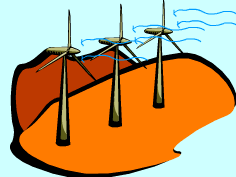 Windmill Capturing the Work Potential in Wind |
Exergy Associated with Kinetic Energy (ke) Kinetic energy is a form of mechanical energy and it can be converted to work entirely regardless of the situation of its surroundings. Thus, exergy of kinetic energy equals the kinetic energy itself, xke = ke = V2/2 where V is the velocity relative to its surroundings. Windmills are equipments to capture the exergy in air blowing through them and use it to do work, like generating electric power.
|
|||||||||||||||||||
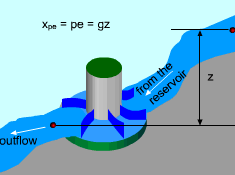 Hydroelectric Turbine Capturing the Work Potential in Elevated Water |
Exergy Associated with Potential Energy (pe) Potential energy is a form of mechanical energy and it can be converted to work entirely regardless of the situation of its surroundings. Thus, exergy of potential energy equals the kinetic energy itself, xpe = pe = gz where g is the gravitational acceleration and z is the elevation of the system relative to a reference level in the surroundings. A hydroelectric turbine is a good example of using exergy of elevated water to generate electric power. |
|||||||||||||||||||
Exergy Associated with Internal Energy (u) Internal energy is the energy associated with the random, disordered motion of molecules. Normally, for most substances with no phase change involved, internal energy is only a function of temperature, and it can be transferred to or from a system as heat whenever there is a temperature difference between the system and its surroundings. The second law states that heat cannot be fully converted to work. This means that exergy associated with internal energy is less than the internal energy itself. A stationary,
simple compressible closed system only possesses internal energy. In
order to figure out the work potential of internal energy, consider a
stationary
simple compressible closed system which is initially at a specified
state(P, T) that undergoes a reversible process to a dead
state(P0, T0). The useful work delivered during
this process is the exergy of the system at its initial state, which
equals the exergy of the internal energy of the system. |
||||||||||||||||||||
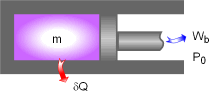 Piston-cylinder Device |
A piston-cylinder device with a fluid of mass m is a simple compressible closed system. The initial and final states of this system are:
A reversible heat engine absorbs heat δQ from the piston-cylinder device when the fluid expands to do work δWb. The reversible heat engine produces work WHE and rejects the waste heat to the surroundings. The total useful work (δWt,u) is the sum of the useful work produced by the piston-cylinder device (δWb,u) and the work produced by the heat engine (WHE). δWt,u = δWb,u + WHE The energy balance of this piston-cylinder device is -δQ = δWb +
dU |
|||||||||||||||||||
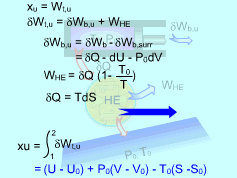 Exergy of Internal Energy |
The surroundings work is δWb,surr = P0dV Hence, δWb,u = δWb - δWb,surr = -δQ - dU - P0dV The thermal efficiency of a reversible heat engine working between a source at temperature T and a sink at temperature T0 is ηth= 1- T0/T The work produced by this heat engine is WHE = δQηth = δQ(1- T0/T) Substitute δWb,u and WHE to the relation of the total useful work yields δWt,u = δWb,u +
WHE Since the piston-cylinder device undergoes a reversible process, the differential heat transfer δQ can be expressed as δQ = TdS The total useful work becomes δWt,u = -dU - P0dV + T0dS Integrate the differential total useful work from the initial state to the final state gives, Wt,u = (U - U0) +P0(V - V0) - T0(S - S0) The exergy of the system at its initial state equals the total useful work. On a unit mass basis, it is xu = (u - u0) +P0(v - v0) - T0(s - s0) This is the exergy associated with internal energy. |
|||||||||||||||||||
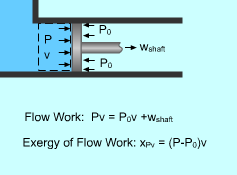 Exergy of Flow Work |
Exergy Associated with Flow Work (Pv) Flow work was defined as the energy needed to push a unit mass of fluid into or out a control volume. it was determined as wflow = Pv where The flow work is essentially a boundary work done on its downstream, and the exergy of flow work equals the exergy of boundary work, which is the difference between the boundary work Pv and the surroundings work P0v. xPv = Pv - P0v |
|||||||||||||||||||
Exergy Associated with Enthalpy (h) Enthalpy is defined as the sum of internal energy and the flow work, which is, h = u + Pv Therefore, the exergy associated with enthalpy is simply the sum of the exergies of internal energy and flow work. That is, xh = xu + xPv |
||||||||||||||||||||