Problem Graphic

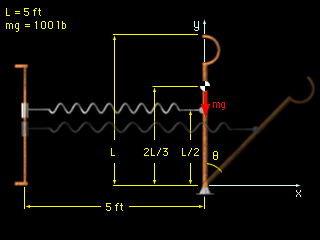
The defending soldiers of a castle are launching a watermelon over the castle wall at an advancing army. To do this, they have designed a catapult with a heavy spring.

What is known:

• The catapult and spring have the dimensions shown.
• The spring constant k is 160 lb/ft, and the spring is in a relaxed position when the catapult is vertical (i.e. the relaxed length is 5 ft).
• The collar of the spring is attached to a frictionless bearing.
• The center of mass of the catapult (without the watermelon) is located at 2L/3.

• If the system is conservative, we can find an equation for the potential energy of the catapult in terms of θ.
• The values of θ that yield zero for the derivative of the potential energy indicate the equilibrium positions for the catapult.
• Use the second derivative of the potential energy to determine which positions are stable, and which are unstable.