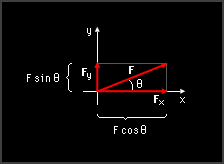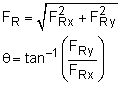| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| 2-D Vectors | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Vector Components |
||
 Vector Components 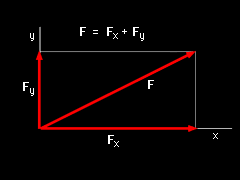 X-Y Axis Orientation
|
In the previous section, vectors were described using its magnitude and direction. This makes mathematical operations difficult (cannot simply add angles). To help solve this problem, vectors are usually split into components. For example, if two vectors, F1 and F2, give the vector F when added together, then F1 and F2 are said to be components of the vector F: F = F1 + F2 If the vectors F1 and F2 are perpendicular to each other, they are called rectangular, or Cartesian, components. If the x-y axis is oriented along these components, they are labeled Fx and Fy respectively: F = Fx + Fy If two vectors, i and j, have a magnitude of one and are in the x and y direction respectively, then F can be written as F = Fxi + Fyj The vectors i and j are called Cartesian unit vectors, and Fx and Fy are the scalar components of the vector F. This configuration is the most common to describe a vector and allows vectors to be added and subtracted quickly and easily. If the angle θ is measured from the x axis counterclockwise, then the scalar components are Fx = F cosθ |
|
| General Unit Vectors |
||
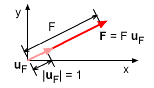 General Unit Vector uF |
Unit vectors in the x and y directions (i and j) where used the above paragraphs, but unit vectors can also be used in any direction. Unit vectors give direction where magnitude gives the length of the vector. Unit vectors are defined as uF = F/F and have a magnitude of 1. |
|
| Vector Addition and Subtraction |
||
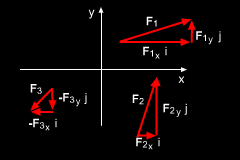 Addition of Multiple Vector
|
When a set of vectors are described using Cartesian unit vectors (i and j), then the resultant vector is just the addition (or subtraction) each components, giving FR = F1 + F2 +... = ΣFxi + ΣFyj where ΣFx = F1x + F2x +... Note, Fn-x and Fn-y are the components of each individual vector where n is the numbering of each vector being added. The magnitude and direction of the resultant vector, FR, can be determined just like any individual vector by, |
|
Practice Homework and Test problems now available in the 'Eng Statics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.