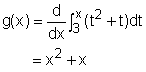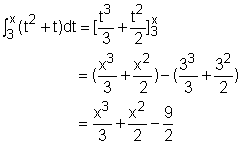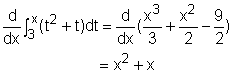This section introduces the Fundamental Theorem of Calculus.

The concept of derivative and integral will be related by the Fundamental Theorem of Calculus. This theorem consists of two parts.

• Part one states:
  If function f is continuous on interval between a and b, then the function g which is defined by
  
           a ≤ x ≤ b
  
  is continuous on the [a,b], differentiable on (a, b), and g ^'(x) = f(x).
  
• Part two states:
  If function f is continuous on the interval between a and b, then
  
                         (1)       
  
  where F is any antiderivative of f, that is F ^'(x) = f(x). The above equation can also be expressed as
  
       

This theorem can be better understood by finding the result of .

The function t² + t is a continuous function over the interval between 3 and x. According to the first part of Fundamental Theorem of Calculus, the derivative of this function is

In order to double check the answer, can be determined by an alternative method. First, use the second part of Fundamental Theorem of Calculus to find the antiderivative of on the interval [3, x].

Next, take the derivative of the result gives

It is clear that both methods give the same results. In order to use the Fundamental Theorem of Calculus effectively, important formulas of antiderivative are given in the table on the left.