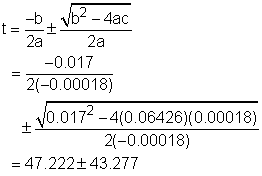| Ch 4. The Mean Value Theorem | Multimedia Engineering Math | ||||||
|
Maximum & Minimum |
Rolle's Theorem |
Mean Value Theorem |
Monotonic Functions |
First Derivative Test |
Concavity & Inflection |
Second Derivative Test |
|
| Maximum and Minimum | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
MATHEMATICS - CASE STUDY SOLUTION
|
||
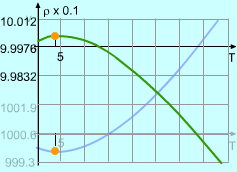
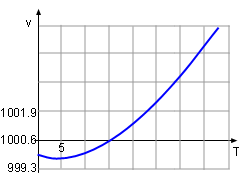 Volume |
Between 0oC and 40oC, the volume, v, of a 1 kg solution was determined to follow the relationship v = 999.87 - 0.06426T + 0.0085T2 - 0.00006T3 where T is the temperature. At what temperature is the mass density a maximum? Let the density, volume and the mass of the solution be ρ, v and m respectively. |
|
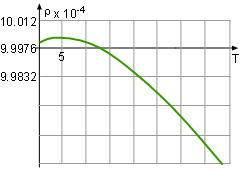 Density |
The density is defined as ρ = mass/volume = m/v = 1000/v.
In order to find the maximum dencisty in the domain between 0oC and 40oC, the following steps need to be taken:
|
|
|
The critical points is the point where the derivative of the density is 0 or does not exist. Therefore, the derivative of the density, ρ, with respect to temperature, T, is needed, Since v is not 0, the critical point of density is the same as the volume and it is easy to calculate the critical point of the volume. The formula of the volume is given v = 999.87 - 0.06426T + 0.0085T2 - 0.00006T3 Differentiate both side of the formula with respect to temperaure gives: dv/dT = - 0.06426 + 0.0170T - 0.00018T2 Find the temperature when dv/dT = 0. - 0.06426 + 0.0170T - 0.00018T2 = 0 So T = 90.5 or T = 3.945 It is given that the range of temperature in the volume function is from 0oC to 40oC, so the 90.5 is discarded and thus 3.945 is the solution. At this temperature, the volume of the solution is v(3.945) = 999.87 - 0.06426T + 0.0085T2 =
999.87 - 0.06426(3.945) = 999.74 The density at temperature 3.945 is ρ(3.945) = 1000/v = 1000/999.74 = 1.0003 With the same method, the density at the temperature of 0 and 40 can be calculated. ρ(0) = 1.0001 ρ(3.945) = 0.993 Comparing the three density, the maximum value is 1.0003 kg/m3 at a temperature of 3.945oC. |
|