| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Trigonometric Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
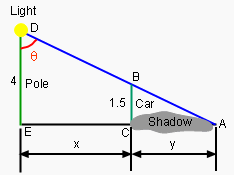 The relationship of the pole, the light and the car |
The speed of the car is 5 m/sec.The height of the pole and the car is 4 and 1.5 meters respectively. How fast does the the angle θ change 1 second after the car starts to move. Let the angle made by the pole, the light and the car be θ. Let the distance from the pole to the car be x. Let the length of the shadow be y. ΔABC is similar to ΔADE, so 1.5/4 = y/(x + y) y = 0.6x x + y = 1.6x In trigonometry, the relationship between x + y and θ is: tanθ = (x + y)/4 = 1.6x/4 = 0.4x |
|
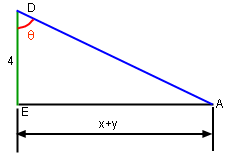 Trigonometry for Finding sec2θ |
Differentiate this relationship with respect to time: sec2θ(dθ/dt) = 0.4dx/dt dθ/dt = 0.4(dx/dt)/sec2θ Notice that the rate of change of the angle, dθ/dt is a function of both the car speed, dx/dt and the current angle. In this case dx/dt = 5 is given, but sec2θ must be determined. 1 second after the car starts, x = (1)(5) = 5 x + y = 1.6(5) = 8 sec2θ(AD/4)2 = (<(x + y)2 +42)/16 = 5 Substituting sec2θ = 5 into θ't =
0.4x't/sec2θ gives |
|