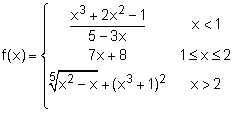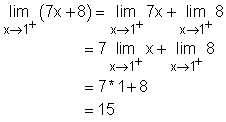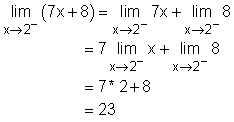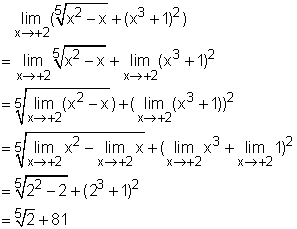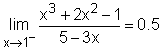| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Limit Laws | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
In a series cutting experiments, Jimmy summarized the relationship between force to cut the material and the heat released from the material. The heat is a piecewise continuous function of force. He wants to analysis the heat released when force is 1 and 2 kN. The function is: Since f(x) is a piecewise function, the functions for f(x) on the left and right hand side of 1 kN and 2 kN. The way to analysis the boundary heat conductive is to consider both side heat conductive at the boundary. First, consider the case of x approaches 1-: |
||
Second, consider the case of x approaches 1+: Third, consider the case of x approaches 2-: Finally, consider the case of x approaches 2+: |
||
| Discussion |
||
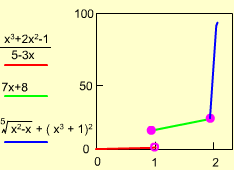 Piecewise f(x) function diagram |
|
|