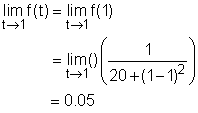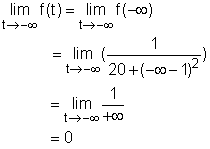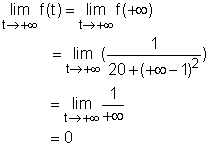| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Limit of a Function | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
The thermal conductivity coefficient of a
material is a function of temperature. What is the coefficient at the
temperature of -∞, 1, +∞. |
||
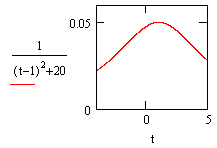 Diagram of f(t) when t is from 0 to 5 |
When t = 1, f(t) = f(1) From the left diagram, it can be found that when t = 1, f(t) is equal
to 0.05. The diagram verifies the previous calculated result. |
|
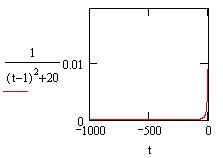 Diagram of f(t) when t is from -1000 to 0 |
When t = -∞, |
|
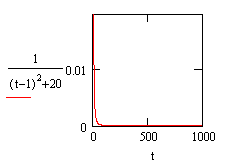 Diagram of f(t) when t is from 0 to 1000 |
When t = +∞, |
|
| Discussion |
||
|
||