| Ch 6. Modeling and Similitude | Multimedia Engineering Fluids | ||||||
|
Dimensional Analysis |
Similitude |
Dimensionless Groups |
|||||
| Common Dimensionless Groups | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
FLUID MECHANICS - THEORY |
||||||||||||||||||||||
|
Some of the dimensionless groups encountered frequently in the study of fluid mechanics are introduced in this section. |
||||||||||||||||||||||
| Common Dimensionless Groups |
||||||||||||||||||||||
|
|
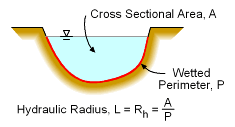
As discussed in another section, dimensional analysis can be used to identify dimensionless groups (pi terms) governing a system. Some common dimensionless groups in fluid mechanics are introduced here. Reynolds Number (Re): The Reynolds number perhaps is the most common dimensionless parameter used in fluid mechanics. It is defined as Re = ρVL/μ where ρ is the density, V is the velocity, L is the characteristic length, and μ is the viscosity. The L term is different for each flow type. For example, for a pipe, L is the diameter of the pipe. For open channel flow, the hydraulic radius, Rh (see diagram) is commonly used. Physically, Re represents the ratio of the inertial force to the viscous force. A small Reynolds number implies that the viscous effects are important, while the inertial effects are dominant when the Reynolds number is large. The Reynolds number is commonly used to characterize if a flow in a pipe is laminar or turbulent. The flow is generally assumed to be laminar when Re < 2,100, and turbulent when Re > 4,000. The flow is referred to as transition flow when the Reynolds number is between 2,100 and 4,000. |
|||||||||||||||||||||
|
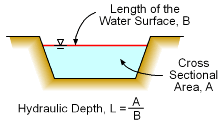
Froude Number (Fr): The Froude number is an important dimensionless parameter in the study of open-channel flow, and it is given by Fr = V / (gL)0.5 where V is the average velocity, L is the characteristic length associated with the depth (hydraulic depth for open channel flow), and g is the gravitational acceleration. For rectangular cross sections, the hydraulic depth is the water depth. Physically, the Froude number represents the ratio of inertial forces to gravitational forces. As discussed in the open-channel sections, open-channel flow can
be classified according to the Froude number in the following manner: It is also common to write Fr as V/c, where c is the wave celerity, c (speed of a wave in the fluid). This form is similar to the Mach Number in air. For subcritical flow (V < c), the waves created by any surface disturbances (e.g., throwing a stone in the water) at the downstream can travel upstream. On the other hand, for supercritical flow (V > c), all surface disturbances will be swept downstream. The wave will remain stationary for critical flow (V = c). |
|||||||||||||||||||||
|
Mach Number (Ma): For high speed flows in some fluids, density is highly dependent on the pressure, and the compressibility effects become important. The Mach number is used to indicate if a flow is incompressible or compressible, and it is given by Ma = V/c where c is the speed of sound (343 m/s at 20oC) and V is the fluid velocity. The Mach number represents the ratio of inertia forces to compressibility forces. Flow can be characterized using the Mach number as folllows: The Mach number is often used to classify the top speed of a fighter or passenger jet. For example, the B-2 bomber shown in the picture is capable of reaching high subsonic speed. The Concorde of British Airways is a supersonic passenger jet, which cruises at Mach 2, and it takes only approximately 4 hours from Los Angeles to Tokyo. Compressible flow is beyond the scope of this introductory fluid mechanics eBook, and is discussed in an advanced level fluid mechanics course. |
|||||||||||||||||||||
Weber Number (We): The dimensionless parameter associated with surface tension effects is the Weber number, and it is defined as We = ρV2L/σ where σ is the surface tension. The Weber number denotes the ratio of the inertial forces to surface tension forces. The Weber number becomes an important parameter when dealing with applications involve two fluid interfaces such as the flow of thin films of liquid and bubble formation. |
||||||||||||||||||||||
|
||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.