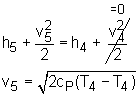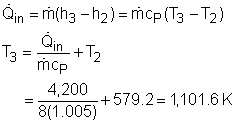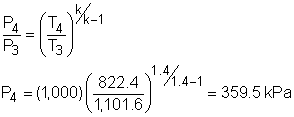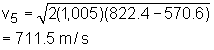A turbojet aircraft is held stationary by the brakes to load seriously injured people. The force applied to the brakes needs to be determined.

Assumptions:

• Model the cycle in the aircraft engine as an ideal jet-propulsion cycle.
• Cold-air-standard assumption is valid for this analysis, so the constant pressure specific heat c_P = 1.005 kJ/(kg-K) and the specific heat ratio k = 1.4.
• The engine operates in steady condition.
• Kinetic and potential energies are negligible, except at the nozzle exit.
• The turbine work output equals the work consumed by the compressor.
• Neglect the effect of the diffuser.
• Neglect the slight increase in mass due to the addition of fuel.

T-s Diagram of the
Ideal Jet-propulsion Cycle

Model the cycle in the aircraft engine as an ideal jet-propulsion cycle. The T-s diagram of the ideal jet-propulsion cycle described is shown on the left.

The braking force equals the thrust developed by the engine when the airplane is stationary. The thrust can be determined by

where
       = mass flow rate of air, given as 8 kg/s
      v_exit = velocity of air at the exit of the nozzle
      v_inlet = velocity of air at the inlet of the engine

The airplane is stationary on the ground and the air velocity at the inlet of the engine is negligible. Also, the effect of diffuser is negligible. Thus, the thrust can be simplified as

The exit velocity of the nozzle can determined by the energy balance of the nozzle. In steady-flow condition, it is

The above analysis shows that in order to calculate the exit velocity, temperatures at state 4 and state 5 need to be determined first.

State 1:
      T₁ = 300 K (given)
      P₁ = 100 kPa (given)

State 2:
      P₂/P₁ = r_P = 10 (given)
      P₂ = P₁r_P = 100(10) = 1,000 kPa

Process 1-2: isentropic compression.

State 3:
Process 2-3: constant pressure heat addition

      P₃ = P₂ = 1,000 kPa

Heat transfer into the cycle equals,

The temperature at state 3 is

State 4:
The work produced by the turbine equals the work consumed by the compressor. Thus,

      h₃ - h₄ = h₂ - h₁
      T₄ = T₃ - (T₂ - T₁ )
          = 1,101.6 - (579.2 -300) = 822.4 K

Process 3-4: isentropic expansion in turbine

State 5:
Process 5-1 is a constant-pressure heat rejection process, thus,

      P₅ = P₁ = 100 kPa

Process 4-5 is an isentropic expansion process in nozzle.

After determining state 4 and state 5, the exit velocity at the nozzle can be determined as

Substitute v₅ and mass flow rate of air into the expression of thrust yields,

      F = 8(711.5) = 5,692 N

To hold the airplane stationary, 5,692 N force needs to be applied to the brakes to balance the thrust developed by the engine.