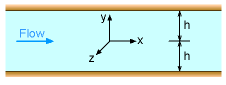| Ch 8. Incompressible and Viscous Flow | Multimedia Engineering Fluids | ||||||
|
Flow between Parallel Plates |
Couette Flow |
Viscous Flow in Pipe |
|||||
| Flow between Parallel Plates | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
In this section, the concepts of laminar
and turbulent flow will be introduced. It should be understood that
only limited problems in viscous flow can be solved analytically.
This section will present one such problem where an exact solution is possible - flow
between infinite parallel plates. |
||
|
|
Laminar and Turbulent Flow |
|
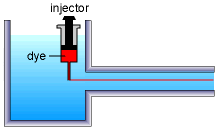
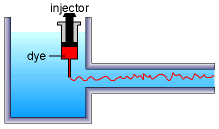
Fluid flow can be classified as laminar or turbulent, which can be best described using the classic Reynolds experiment. Consider water flowing through a transparent pipe from a reservoir. A dye is injected at the inlet of the pipe. For a small flow rate, the dye will remain intact and form a single filament as it moves downstream. This is laminar flow since the dye flows in an ordered fashion. For a large flow rate, the dye will fluctuate immediately in a random fashion due to microscopic variations in the velocity field, and rapid dispersion of the dye is observed throughout the pipe. This is turbulent flow since the dye stream is unstable and fluctuating throughout the flow field. At an intermediate flow rate, the flow is in transition. The dye is intact at the beginning, and it slowly becomes fluctuating as it moves downstream. The fluctuations, however, are not as intense as in fully turbulent flow. Recall that the
Reynolds number (Re) is determined by |
||
| Flow between Fixed Parallel Plates |
||
|
|
Consider steady, incompressible, laminar flow between two infinite parallel horizontal plates as shown in the figure. The flow is in the x- direction, hence there is no velocity component in either the y- or z- direction (i.e., v = 0 and w = 0). The steady-state continuity equation becomes From Eqn. 1, it can be concluded that the velocity u is a function of both y and z only. Since the plates are infinitely wide, it can be argued that the velocity u should not be a function of z, i.e., it must be a function of y only, u = u(y). Applying the Navier-Stokes equations, along with the assumptions that v = 0, w = 0 and u = u(y), yields Eqn. 4 indicates that the pressure is a function of x and
y. Integrate Eqn. 3 to yield Hence it can be concluded that |
|
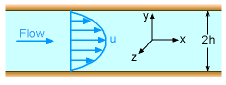 Velocity Profile |
The velocity profile becomes which is a parabola. The total volumetric flow per linear depth can be obtained integrating the velocity to give Note, q is per linear depth, which is different than Q which is the total volumetric flow rate. Also note that the flow is negative, i.e. to the left, for a positive pressure gradient, dp/dx. This is due to the gradient definition where decreasing pressure to the right is negative. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.