Problem Diagram

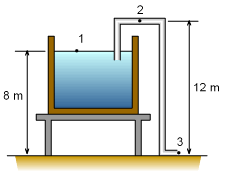
Applying Bernoulli's equation between points 1 and 2 yields

For a large open tank, p₁ = 0 (gage pressure) and V₁ = 0. Rearranging the above equation to gives

Thus the pressure at point 2 can be determined once the velocity at point 2 (V₂) is known. To determine V₂, apply Bernoulli's equation between points 1 and 3, and recognize that the velocity at points 2 and 3 is equal for constant diameter pipe and a steady rate of flow.

The pipe outlet acts as a free jet, so p₃ = 0 (gage pressure), and z₃ = 0 (datum). Thus the velocity at point 2 is then given by

The gage pressure at point 2 thus can be simplified as,

     p₂ = -0.5ρ (2gz₁) + ρg (z₁ - z₂)
         = -ρgz₂ = -(1000)(9.8)(12)
         = -117.6 kPa (gage)

The vapor pressure in terms of the gage pressure is given by

      p_v = 2.34 - 101.3 = -98.96 kPa.

Since p₂ = -117.6 kPa is less than the vapor pressure of -98.96 kPa, cavitation will occur.

To avoid cavitation (i.e., p₂ cannot be less than the vapor pressure), the maximum height of z₂ should be