| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
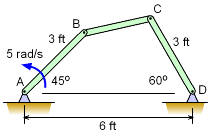 Three Bar Linkage Problem |
Example |
|
|
Bar AB of a classic three bar linkage system has an angular velocity of 5 rad/s. The lengths of the bars AB and DC are each 3 ft. What is the angular velocity of bar BC?
|
||
| Solution |
||
|
|
This is a three step process. First find the velocity of point B. Then find the direction velocity direction of point C. Finally, the angular velocity of bar BC can be determined the information known about point B and C. Velocity of point B, Velocity of point C, Angular velocity of bar BC is found by relating the velocity of point C to point B, Solving i and j terms, Solving equations for ωBC, |
|
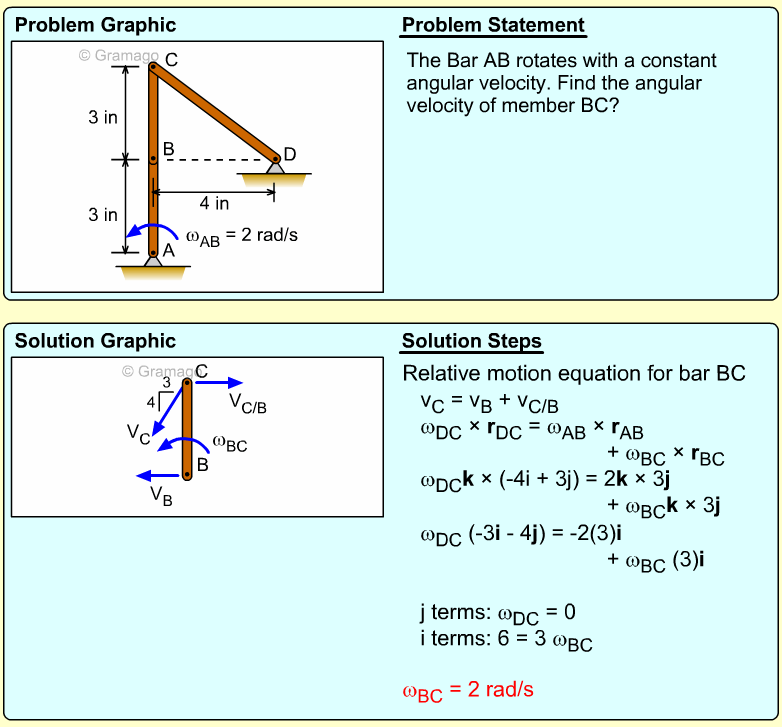
| Example Problem 1 |
||
|
||
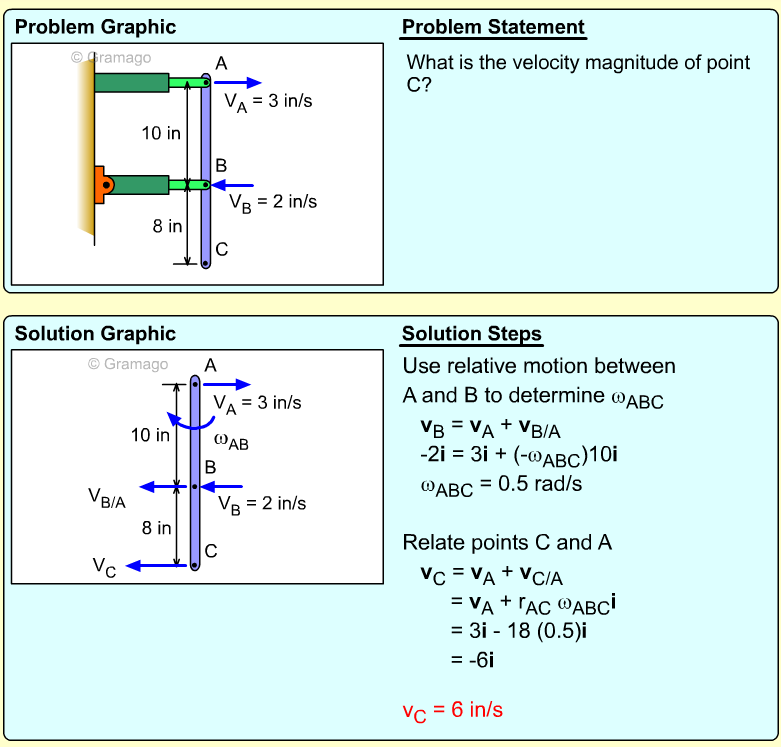
| Example Problem 2 |
||
|
||
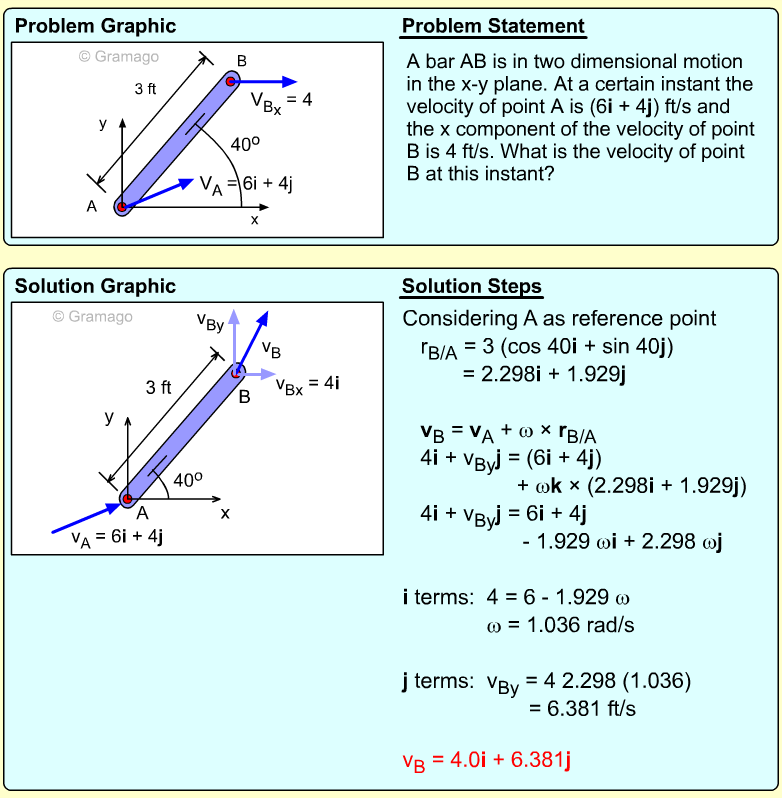
| Example Problem 3 |
||
|
||
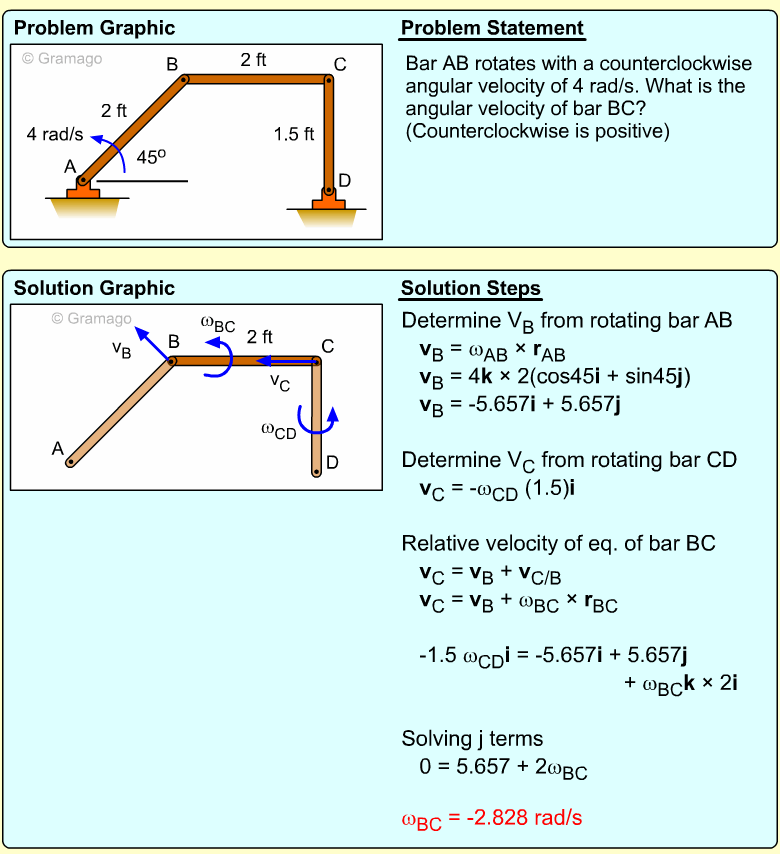
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||
| Example Problem 10 |
||
|
||
| Example Problem 11 |
||
|
||
| Example Problem 12 |
||
|
||
| Example Problem 13 |
||
|
||
| Example Problem 14 |
||
|
||
| Example Problem 15 |
||
|
||