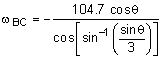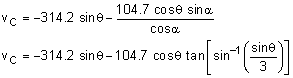| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
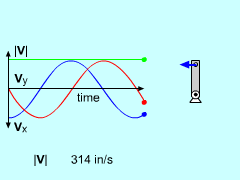
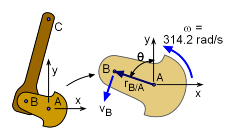
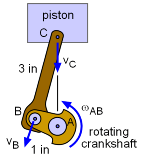 Piston Configuration Labels |
This piston problem can be solved by breaking the problem into two parts.
After the velocity of point C is known in terms of the rotation angle θ, the problem could be optimized to find the maximum velocity. |
|
| Part a) Motion of Bar AB |
||
|
|
Use the relative velocity equation to find the velocity of B. Note that point A does not translate. vB = vA + vB/A = 0 + ωAB × rB/A Next, the angular velocity, ω = 3,000 rpm, needs to be converted into radians per second. 3000 rpm (1 min/60 s) (2π/1 rev) = 314.2 rad/s The relative distance vector now needs to be defined. Referring to the diagram, we get rB/A = -|rB/A| sinθi + |rB/A| cosθj = -1" sinθi + 1" cosθj = -sinθi + cosθj Substituting this into the relative velocity equation above gives the final velocity of point B in terms of the angle θ. The angle θ is still not known but will be determined when the maximum velocity is found. vB = 314.2k × ( -sinθi + cosθj ) = -314.2 cosθi - 314.2 sinθj in/s |
|
| Part b) Motion of Bar BC |
||
|
|
Once again, the relative velocity equation is used to determine the velocity of a point on a rotating and translating bar. vC = vB + vC/B = vB + ωBC × rC/B The velocity of point B is known from previous analysis and the velocity of point C is constrained in the vertical direction. The angular velocity ωBC is not known. vCj = -
314.2 cosθi - 314.2 sinθj + Completing the cross product and equating the i and j components gives, i: 0 = -314.2 cosθ - 3ωBC cosα j: vC = -314.2 sinθ + 3ωBC sinα The two angles θ and α are actually related (see diagram). The horizontal distance of both arms must equal each other since points A and C always aligned in the vertical direction. (3 in) sinα = (1 in) sinθ Substituting α = sin-1 (sinθ /3) into the i terms and solving for ωBC gives, gives This can now be used with the j terms to solve for the velocity of C in terms of the angle θ, |
|
| Finding Maximum Velocity of Point C |
||
|
|
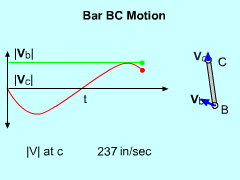
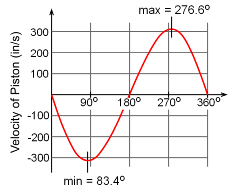
Up to this point, the velocity vC has been derived for any angle θ. The angle that gives the maximum velocity now needs to be determined. This can be done by taking a derivative with respect to the angle θ and equating it to zero. Without the help of a symbolic math program such as Mathcad™ or Mathematica™, closed-form derivation becomes nearly impossible. Even then, the result is complex. The final solution, using numerical methods, for the maximum velocity of point C is θ = 1.455 rad = 83.4o vmax = +/- 316.3 in/s The velocity curve is plotted for point C in the diagram at the left. |
|