| Ch 5. Fundamental Laws (Differential) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Navier-Stokes and Euler's |
Conservation Energy |
|||||
| Conservation of Mass | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Example |
||
|
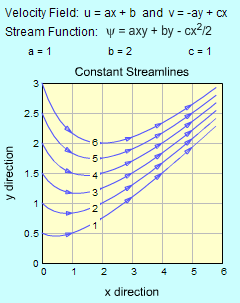
What is the stream function for the following velocity field u = ax + b where a, b and c are arbitrary constants? Also, plot the streamlines where the stream function, ψ, equals 1, 2, 3, 4, 5 and 6. |
||
| Solution |
||
|
|
A few assumptions need to be made before the stream function can be determined. First, the flow is assumed to be steady and compressible. Next, the flow is only in the x and y plan (no z-direction flow). Finally, the velocity field needs to satisfy the continuity equation, For the given velocity field, the continuity equation becomes, (a) + (-a) = 0 which satisfies the continuity equation. Recall, the stream function, ψ, is a single function that satisfies both functions, Substituting the horizontal velocity, u, and integrating gives, ψ = axy + by + h(x) where h(x) is any function of x (not y). Now, use this function with the vertical velocity, v, to give -ay + cx = -[ ay + 0 + h'(x) ] where h'(x) is simply d[h(x)]/dx. The "ay" terms cancel giving, h'(x) = -cx |
|
|
Integrating h'(x) gives h(x) = -cx2/2 + G where G is any arbitrary constant which will be set to zero for easy plotting. The final form of the stream function is ψ = axy + by - cx2/2 + G The stream function can be plotted by setting G to 0 (or to any arbitrary value) and then setting ψ to a series of different values. Each ψ value represents a streamline where the velocity is tangent to that streamline. The graph at the left plots six different streamlines, ψ = 1, 2, 3, 4, 5, and 6. The velocity field equations has three coefficients, a, b, and c. The interactive graph permits these terms to be changed to see their effects on the streamlines. There are infinite number of streamline, and only six have been plotted to represent the flow pattern for the given velocity field. |
|