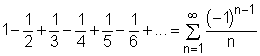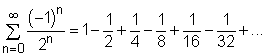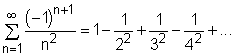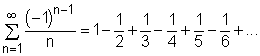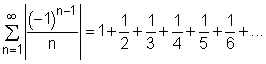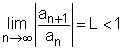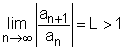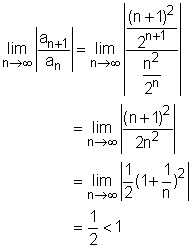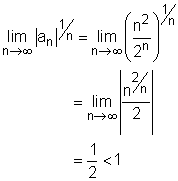| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Alternating Series and Absolute Convergence | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
The series introduced thus far have been
those with non-negative terms. In this section, series with mixed signs
such as the alternating series will be introduced. Several convergence
testing methods, such as the alternating series test, ratio test and
root test, will be presented. |
||
| Alternating Series |
||
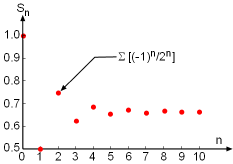
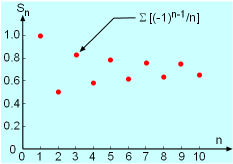 The Plot of the Partial Sum for an Alternate Harmonic Series Σ[(-1)n-1/n] as a Function of n. |
As the name of the alternate series imply, these series have consecutive terms with alternate signs. An example of alternating series is The above series is also known as the alternating harmonic series. Note
that the last term of the series has the form an = (-1)n-1bn where
bn is positive. The plot of the partial sum as a function
of n is shown in the figure on the left. |
|
| Alternating Series Test |
||
|
According to the alternating series test,
when a series consists of Take the series |
|
| Absolute Convergence Test |
||
|
A series Σan is
said to converge absolutely if the series of absolute terms ( For example, the series is absolute convergent since it was proved previously, using the basic comparison and integral tests, that the following series (p-series with p = 2) converges. |
|
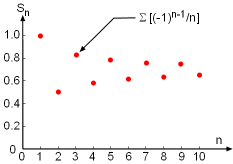 The Plot of the Partial Sum for an Alternate Harmonic Series Σ[(-1)n-1/n] as a Function of n. |
On the other hand, the alternating harmonic series diverges. |
|
| Ratio Test |
||
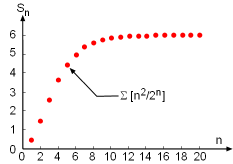 Plot of the Partial Sum for a Series Σ[n2/2n] as a Function of n. |
Another useful test in examining whether a series is convergent or divergent is the ratio test, which is stated as follows: (1) The series (2) The series Note that if the limit tends to 1 then the ratio test gives no information regarding the convergency. The ratio test is particularly useful when examining series with terms that consist of factorials and nth powers of constants. Take the series Hence, this series is absolutely convergent. |
|
| Root Test |
||
Besides the ratio test, the root test can also be used to examine if a series is convergent or divergent. The root test is convenient in determining series with terms raised to the nth power, and it is stated as follows: (1) The series (2) The series The series it is also determined that the series is absolute convergent. |
||