| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Sequences and Series | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
David has 80,000 dollars in his college fund, but he can only make one withdrawal for half of the remaining fund each month. Let a1, a2 , a3, ... an be
the amount of withdrawal and Each month, David can withdraw: a1 = (60,000)(1/8) The remaining balance becomes: d1 = (60,000)(1 - 1/8) = (60,000)(7/8) |
||
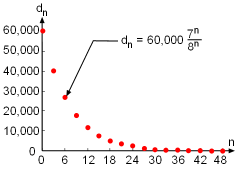 The Plot of Remaining Balance versus Month |
Thus, a sequence can be formed to represent the remaining balance of the fund: dn = {60,000(7/8, 49/64, 343/512,..., (7/8)n)} As the number of month increases, the balance remaining becomes closer and closer to 0. However, it is assumed that the college fund runs out when the remaining balance is one hundred dollars. Hence, the problem at hand is what value of n will give the sequence a limit of 100. That is, (60,000)(7/8)n = 100 Solving the above equation to obtain: n = 47.9 Hence, David has around 48 months to prepare and become financially independent. |
|