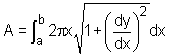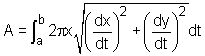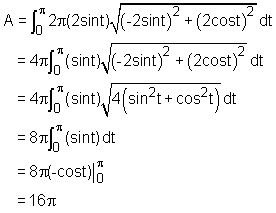| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Surface Area | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
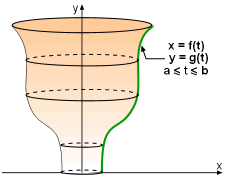
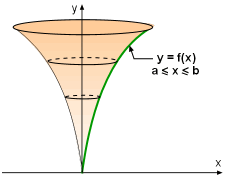 Surface of Revolution |
When a curve y = f(x) for a ≤ x ≤ b is rotated about the y-axis, the surface of revolution is given by |
|
| Surface Area: Parametric Form |
||
|
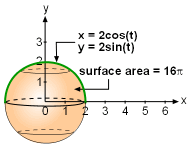
Similar to the concept of an arc length, when a curve is given by the following parametric equations x = f(t) and y = g(t) for a ≤ t ≤ b, the surface area of revolution for the curve revolving around the y-axis is defined as Consider a sphere with a center at (0,0) and radius of 2. The sphere can be obtained by rotating a semi-circle x = 2cos(t) and y = 2sin(t) for 0 ≤ t ≤ π about the x-axis. According to the definition of the surface of revolution, the surface area of the sphere is given by |
|