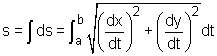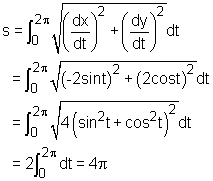| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Arc Length | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
 Arc Length |
It is known that if a smooth curve can be described using the function y = f(x) for a ≤ x ≤ b, then the arc length is defined as The arc length for a curve described using parametric equations will be introduced in this section. |
|
| Arc Length - Parametric Equation |
||
|
When a curve is given using the following parametric equations x = f(t) and y = g(t) for a ≤ t ≤ b, the arc length of the curve is defined as where ds is the differential arc length. The expression for the differential arc length is Note that the definition of the arc length is based on the assumption that both dx/dt and dy/dt are continuous. The arc length is basically the sum of the differential arc length ds along the curve. Consider a circle with its center at (0,0) and a radius of 2 inches given by the following parametric equations as shown in the figure. x = 2cos(t) and y = 2sin(t) for 0 ≤ t ≤ 2π According to the definition of the arc length, the circumference of the circle is given by: |
|