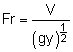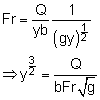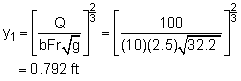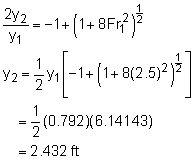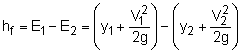| Ch 10. Open-Channel Flow | Multimedia Engineering Fluids | ||||||
|
Uniform Flow |
Gradually Varied Flow |
Rapidly Varied Flow |
|||||
| Rapidly Varied Flow | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Questions |
||
|
|
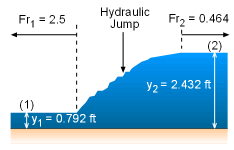
Downstream conditions for a rectangular concrete channel (b = 10 ft) are forcing a hydraulic jump. If Q = 100 cfs and the upstream Froude number is 2.5, find the horsepower lost in the jump. Assume steady flow. |
|
| Solution |
||
The Froude number is defined as where V = Q/A = Q/yb Rearranging the equation to yield The upstream water depth and velocity are determined as follows: Using the following equation derived from the conservation of momentum, the depth after the jump can be calculated (for rectangular channel only): |
||
 Hydraulic Jump Conditions for this Example |
V1y1 = V2y2 for steady flow, thus The dissipation head loss across the jump is given by (assuming flat bottom channel, i.e., Δz = 0) Using the sequent depth relationship for rectangular channel Power dissipated = ρgQhf Since 1 hp = 550 ft-lb/s, Power dissipated = 3,573/550 = 6.5 hp |
|