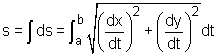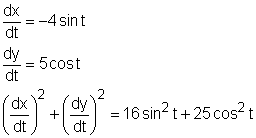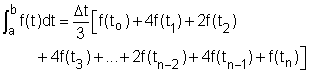| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Arc Length | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
Recall that when a curve is given using the following parametric equations x = f(t) and y = g(t) for a ≤ t ≤ b, the arc length of the curve is defined as The ellipse describing the planet's orbit is x = 4 + 4cos(t) and y = 5 + 5sin(t) The first step is to evaluate the derivatives of the integral as, The arc length of the ellipse is given by: Since there is no obvious technique to perform the closed form integration, a numerical method called the Simpson's Rule is used. According to the Simpson's Rule, an integration can be approximated as follows: where n is even and Δt = (b - a)/n In this case, let The values of f(t) subject to different values of t are summarized in the table on the left: The integration can then be evaluated to give the distance of a complete orbit as |
|||||||||||||||||||||||||||||||||||||