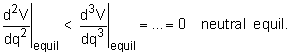| Ch 10. Virtual Work & Potential Energy | Multimedia Engineering Statics | ||||||
|
Virtual Work |
Potential Energy | ||||||
| Potential Energy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Conservative Forces |
||
 Conservative Forces |
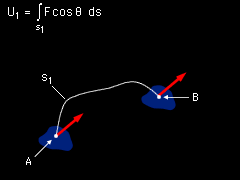
When a force is displaced over a path with a finite length s, the work done can be found by integrating the differential work over the path as If the total work of a force is independent of the path s, then the force is said to be a conservative force. Gravity and spring forces are examples of conservative forces, but friction is nonconservative |
|
| Gravitational Potential Energy |
||
 Gravitational Potential Energy |
The gravitational potential energy of a body is defined as the weight of the body times the distance y above a horizontal reference line, Vg = Wy = mgy If the body is below the reference line, it will have a negative potential energy. |
|
| Elastic Potential Energy |
||
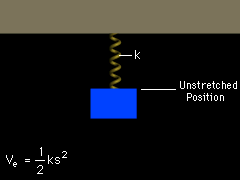 Spring Elastic Potential |
The elastic potential energy of a spring is given by Ve = 1/2 ks2 Here k is the spring constant and s is the distance the spring is stretched or compressed from its unstretched length. |
|
| Potential Energy and Equilibrium |
||
|
If a body is subject to only gravitational and elastic forces, the total potential energy, also called the potential function V, is given by V = Vg + Ve For a single-degree-of-freedom system at a point of equilibrium, the rate-of-change of total potential energy with respect to displacement goes to zero. For a small displacement q (q can be either distance or rotation), this can be stated mathematically as dV/dq = 0 From this equation, the equilibrium position can be determined. |
||
|
Potential Energy and Stability |
|
|
|
A body in equilibrium is said to be in one of three states: stable, neutrally stable, or unstable. After we determine the equilibrium condition, we can determine the stability of that condition from the second derivative of the potential function. If the second derivative of the potential function V is greater than zero, the body is in a stable equilibrium: |
|
 Unstable Equilibrium |
If the second derivative is less than zero, the body is in an unstable equilibrium: |
|
 Neutrally Stable Equilibrium |
If the second derivative is zero, higher-order derivatives must be used to determine the stability. Only if all derivatives of V are zero is the body neutrally stable: |
|