| Ch 10. Virtual Work & Potential Energy | Multimedia Engineering Statics | ||||||
|
Virtual Work |
Potential Energy | ||||||
| Potential Energy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
|
|
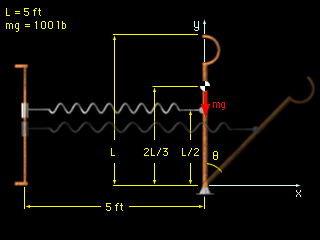
The only forces acting on the catapult are the spring force and the force of gravity. Since both of these are conservative forces, the system is conservative, and the potential energy can be used to determine equilibrium positions and stability. Begin with a free-body diagram with the origin of the x-y coordinate system located at the pivot point of the catapult. |
|||||||
|
||||||||
| Equilibrium |
||||||||
|
|
The equilibrium positions for the catapult can be found by taking the first derivative of the potential energy, dV/dθ = -2/3 mgL sinθ + 1/4 L2 k sinθ cosθ When the catapult is in equilibrium, the derivative of the potential energy is zero. dV/dθ = 0 There are three values of θ for which the catapult is in equilibrium. The first is relatively easy to determine as L sinθ = 0 The second and third values can be found by setting the expression in parenthesis equal to zero. 1/4 Lk cosθ - 2/3 mg = 0 |
|||||||
| Stability |
||||||||
|
|
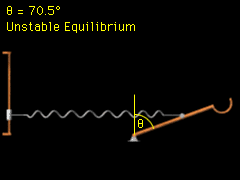
To determine the stability of the three equilibrium positions, take the second derivative of the potential energy. d2V/dθ2 = L cosθ (1/4 Lk cosθ - 2/3 mg) Next, substitute θ = 0° into the equation for the second derivative of the potential energy which gives, d2V/dθ2 = L (1/4 Lk - 2/3 mg) > 0 Because the second derivative of the potential energy is greater than zero, θ = 0 is a stable equilibrium position. Now, substitute θ = ±70.5 into the equation for the second derivative of the potential energy. d2V/dθ2 = L cos70.5 (1/4 Lk cos70.5 - 2/3 mg) d2V/dθ2 < 0 Because the second derivative of the potential energy is less than zero, θ = ±70.5° are unstable equilibrium positions. |
|||||||