| Ch 10. Virtual Work & Potential Energy | Multimedia Engineering Statics | ||||||
|
Virtual Work |
Potential Energy | ||||||
| Virtual Work | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Work of a Force |
||
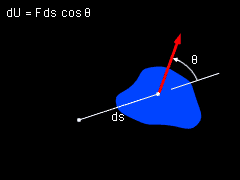 Work of a Force |
A force does work when it undergoes a displacement in the direction of the force. If a force moves a small distance dr, the work done by the force is given by dU = F • dr If the angle between the force and the vector dr is θ, then the scalar equation is dU = F ds cosθ Here ds is the magnitude of the vector dr. |
|
| Work of a Couple |
||
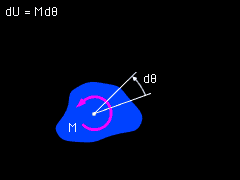 Work of a Couple |
A couple, or moment, does work when it undergoes a rotation in the plane of the couple. If the couple rotates a small angle dθ, then the work done by the couple is given by dU = M = dθ If the rotation takes place in the plane of the couple, then the scalar equation is dU = M dθ |
|
| Virtual Work |
||
 Virtual Work of a Force |
The virtual work of a force or couple is defined as the work done by an imaginary or virtual displacement. In scalar notation, the virtual work of a force is given by δU = F δs cosθ In x and y components, δU = Fx δx + Fy δy Here Fx and Fy are the forces in the x and y directions, and δx and δy are the virtual displacements in the x and y directions. The virtual work of a couple, or moment, is δU = M δθ |
|
| Principle of Virtual Work |
||
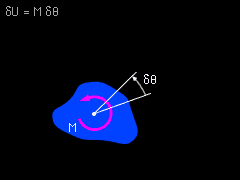 Virtual Work of a Couple |
The principle of virtual work states that a system of rigid bodies is in equilibrium if the total virtual work done by all external forces and couples acting on the system is zero for each independent virtual displacement of the system. Mathematically, this means that equilibrium for a single-degree-of-freedom system is δU = 0 From this equation, the equilibrium position or equilibrium forces can be determined. |
|