| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Parametric Equations | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||||||||
|
|
In the previous
section, curves were defined by providing a relation between x
and y [i.e., y = f(x) or x = g(y)]. Another method, which can be used
to describe curves, is by means of the parametric equations. |
|||||||||||||||||||
| Parametric Equations |
||||||||||||||||||||
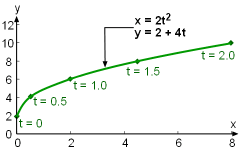
| Table:
Data for the Parametric Equations x = t2 and y = 2 + 4t
| Some curves (e.g., cycloid, which is traced
by rolling a circle along a flat surface) are easier to describe using
a pair of parametric equations. The coordinates x and y of the curve
are given using a third variable t, such as where t is referred to as the parameter. Hence, for a given value of t, a point (x,y) is determined. For example, let t be the time while x and y are the positions of a particle. The parametric equations then describe the path of the particle at different times. The curve shown on the left is defined using the following parametric equations: x = 2t2 |
|||||||||||||||||||