| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Parametric Equations | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||||||||||||||||||||
|
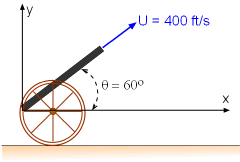
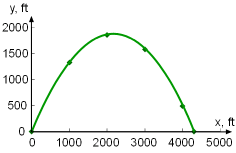
Recall, the path of the projectile was given as by the following parametric equations: x = (Ucosθ)t For U = 400 ft/s and θ = 60o, the parametric equations reduce to: x = (400 cos 60)t = 200t When the projectile hits the ground, y is zero. Thus, 346.4t - 16.1t2 = 0 The corresponding x-position of the projectile is x = 200(21.52) = 4,304 ft Based on the parametric equations, the positions of the trajectory are determined by varying the time t. The trajectory of the projectile is plotted in the figure shown on the left. |
||||||||||||||||||||||