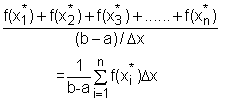| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Average Value of a Function | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Average Value of a Function |
||
|
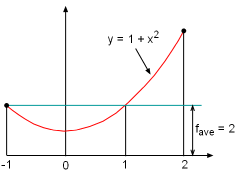
In many situations, the average value of a group of discrete numbers is needed. This is easy to calculate as have = (h1+ h2+ h3+ ...... + hn)/n But, sometimes the average value of a continuous function f(x) on a domain [a, b] needs to be determined. For example, the average atmospheric temperature over 24 hours. To determine the average value of a continuous function, first, the domain [a, b] is divided into n equal subintervals, with equal width, Δx =
(b - a)/n |
|
|
Then points x1* , x2*, x3*, ......, xn* in each subinterval are used to calculate the average value of each subintervals as f(x1*), f(x2*), f(x3*), ......, f(xn*): Since Δx = (b - a)/n, the above expression becomes According to the definition of definite integral, the limiting value of the above summation is Therefore, the average value of a continuous function f(x) on the interval [a, b] is defined as |
|
| Mean Value Theorem for Integrals |
||
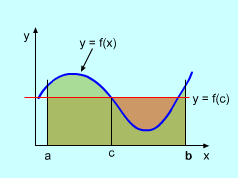 Geometric Interpretation of the Mean Value Theorem for Integrals |
If function f(x) is continuous on [a, b], then there exist a number c in [a, b] such that This is called the Mean Value Theorem for Integrals. The geometric interpretation of the Mean Value Theorem for Integrals is that, for a positive function f(x), there exists a number c between a and b such that the rectangle with base [a, b] and height f(c) has the same area as the region under the graph of f(x) from a to b. |
|