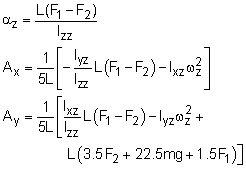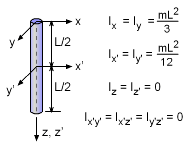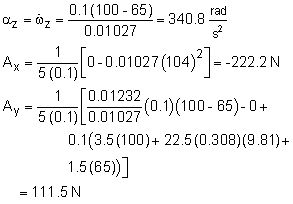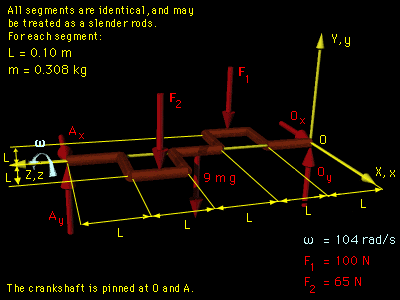
Begin with a diagram at the instant the crankshaft is in the horizontal plane.

Since the principal axes of inertia are not readily known for either the center of gravity or point O, let the reference frame xyz be located at point O as shown,

Problem Geometry

The crankshaft only rotates about the z-axis,

     ω_x = ω_y = 0,       ω_z = ω = 104 rad/s
     

The angular equations (Eqs. 1 in the theory section) simplify to

    ΣM_x = I_yz ω_z² - I_xz α_z²
    ΣM_y = -I_yz α_z² - I_xz ω_z²
    ΣM_x = I_zz α_z²

The moments are due to forces F₁, F₂, A_y and A_x,

     -A_y (5L) + F₂ (3.5L) + 9mg (2.5L) + F₁ (1.5L)
                 = I_yz ω_z² - I_xz α_z²
     A_x (5L) = -I_yz α_z² - I_xz ω_z²
     F₁ L - F₂ L = I_zz α_z²

These equations can be rearranged in terms of the three unknowns A_x, A_y, and α_z, giving

Moment and Product of Inertia
for a Slender Rod

Crankshaft split into Nine Sections

Rotating Reference Axis

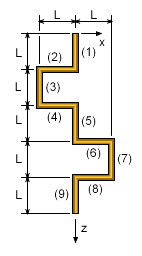
To solve these three equations, the inertia terms, I_zz, I_yz, and I_xz, need to be determined. To find the inertia terms, split the shaft into 9 straight slender rods. The total moment of inertia and product of inertia terms can be found by summing the inertia of all sections about themselves, and using the parallel axis theorem. This gives,

     I_zz = I_zz-1 + I_zz-2 + I_zz-3 + I_zz-4 +
              I_zz-5 + I_zz-6 + I_zz-7 + I_zz-8 + I_zz-9
         = 0 + mL²/3 + (0 + mL²) + mL²/3 +
              0 + mL²/3 + (0 + mL²) + mL²/3 + 0
         = 3.333 mL²
         = 3.333 (0.308 kg) (0.100)²
         = 0.01027 kg-m²

     I_yz = 0 (all sections in x-z plane at given instant)

     I_xz = 0 + (-L/2)(L)m + (-L)(1.5L)m + (-L/2)(2L)m +
              0 + (L/2)(3L)m + (L)(3.5L)m + (L/2)(4L)m + 0
         = 4 mL²
         = 4 (0.308 kg) (0.100)²
         = 0.01232 kg-m²

Substituting the inertia terms and known forces, F₁ = 100 N, and F₂ = 65 N, gives